これなら分かるEMアルゴリズム③
さて,EMアルゴリズムの最終回. 今回は第1回で扱った混合分布モデルの最尤推定と,第2回で扱ったEMアルゴリズムの一般系のつなぎについて書いていきたいと思っている. と言いつつも,実はほとんどの要点は今までの記事に散りばめられている. なので今回はそのまとめの回と考えていただきたい. なお,前回,前々回の記事をご覧になっていない読者の方は以下の記事を参考にしてくださいませ.
混合分布モデルの最尤推定とEMアルゴリズム一般形の関係
まず混合分布モデルの最尤推定の問題では,以下の最適化問題を解くことがゴールだった: $$ \max_{ \bf{1}^\top \bm{\pi} = 1} \sum_{i = 1}^n \log p(\bm{x}_i | \Theta) = \max_{ \bf{1}^\top \bm{\pi} = 1} \sum_{i = 1}^n \log \left( \sum_{k=1} ^K \pi_k p(\bm{x}_i | \bm{\theta}_k) \right). \tag{1} $$ EMアルゴリズムの一般形では,上記のような最尤推定が解けない場合を想定し,潜在変数$\bm{Z}$を導入した. では,混合分布モデルの場合はどのような潜在変数を導入すれば良いのだろうか.
そこで,以下を満たすような潜在変数$Z_i$を導入する. ただし,$Z_i$は$1, 2, \ldots, K$のうちのいずれかの値をとるとする. 気持ちとしては...
- 混合分布モデルをモデリングするとき,各々のデータがどのクラスタ由来であるかを明示したい.
- しかし,現状のモデルの仕方だと,どのデータがどのクラスタ由来なのかは不明である.=> これが潜在変数になる!!!
- $Z_i = k$は,「データ$i$は,クラスタ$k$から由来する」ことを意味指す.
「各データがどのクラスタ由来なのか」という情報が隠れて潜んでいるから,これが潜在変数になるというわけだ. ふむふむ.
さて,導入した潜在変数についての確率モデルは以下のようになる(突然なんでこんな式出てくるの?と思う人もいると思うが,上で書いた潜在変数の「気持ち」をしっかり汲んであげれば以下の解釈もすんなり受け入れられるだろう):
- 事前分布: $p(Z_i = k) = \pi_k$
- $Z_i$のもとでの$\bm{x}_i$の分布: $p(\bm{x}_i|Z_i = k, \Theta) = p(\bm{x}_i | \bm{\theta}_k)$
- $Z_i$と$\bm{x}_i$の同時分布: $p(\bm{x}_i, Z_i = k | \Theta) = p(\bm{x}_i|Z_i = k, \Theta) p(Z_i = k)$
- $Z_i$の事後分布: $p(Z_i = k|\bm{x}_i, \Theta) = \dfrac{p(\bm{x}_i, Z_i = k | \Theta)}{\sum_{l=1}^K p(\bm{x}_i, Z_i = l | \Theta)}$
事後分布の計算はただのベイズの定理であることに注意! なお,第1回の記事でこれが分類問題の場合に$p(y=k|\bm{x})$的な説明をわざと入れたのは,実はこの気持ちを知って欲しいからである. 3回の記事全てを読んでくださった読者はこの気持ちをきっと汲んでくれたはずw
E-Step
道具は揃ったので,以下では実際にEMアルゴリズムの一般形をもとに,混合分布モデルの最尤推定アルゴリズムを再構築してみよう. まずはE-Step. E-Stepでは,$\Theta = \Theta'$に固定し,$q(Z_i = k) = p(Z_i = k|\bm{x}_i, \Theta')$を計算すれば良い. これは上の考察から実はもう答えは出ている. ここでは,混合正規分布モデルの場合における計算を下にのせる: $$ \begin{aligned} q(Z_i = k) = p(Z_i = k|\bm{x}_i, \Theta') &= \dfrac{p(\bm{x}_i, Z_i = k | \Theta')}{\sum_{l=1}^K p(\bm{x}_i, Z_i = l | \Theta')} \\ &= \dfrac{p(Z_i = k) p(\bm{x}_i | Z_i = k, \Theta')}{\sum_{l=1}^K p(Z_i = l) p(\bm{x}_i | Z_i = l, \Theta')} \\ &= \dfrac{\pi_k' \mathcal{N}(\bm{x}_i|\bm{\mu}_k', \varSigma_k')}{\sum_{l=1}^K \pi_l' \mathcal{N}(\bm{x}_i|\bm{\mu}_l', \varSigma_l')}. \end{aligned} $$ さて,第1回の記事を真面目に読んでいただいた方はここで気づくかもしれない. そう,ここの$q(Z_i = k)$だが,これは実は第1回の記事で導入した$q_k^{(i)}$に対応しているのである.
M-Step
次にM-Stepについてだが,これは以下の最適化問題を解けば良いのであった: $$ \begin{aligned} \theta' = \operatorname{argmax}_{\theta} Q(\theta, \theta') = \operatorname{argmax}_{\theta} \sum_{\bm{Z}} p(\bm{Z}|\bm{X}, \theta') \log p(\bm{X}, \bm{Z}|\theta). \tag{2} \end{aligned} $$ 混合正規分布の場合,この最適化問題の目的関数は以下のようになる: $$ Q(\theta, \theta') = \sum_{i=1}^n \sum_{k=1}^K q(Z_i = k) \log \Big( \pi_k \mathcal{N}(\bm{x}_i|\bm{\mu}_k, \varSigma_k) \Big). $$ さて,この式と第1回の記事の(4)式を比べてみて欲しい. いま,$q_k^{(i)}$が固定されていることに注意すると,この両者は全く同じ最適化問題を解いていることが分かる. ゆえに,第1回の記事同様,ラグランジュ関数を作って微分して,最適性条件を調べれば(2)の最適化問題は解けるということになる. これで,M-Stepにおける対応関係も確認できた.
まとめ
さて,最後に一般版EMアルゴリズムと,混合正規分布モデルにおけるEMアルゴリズムのまとめを以下に記しておく.
| 一般版 | 混合正規分布モデル版 | |
|---|---|---|
| 初期化 | $\theta'$を初期化 | $\pi_k, \bm{\mu}_k, \varSigma_k$の初期化 |
| E-Step | $q(\bm{Z}) = p(\bm{Z} | \bm{X}, \theta')$を計算 | $q(Z_i = k) = \dfrac{\pi_k' \mathcal{N}(\bm{x}_i|\bm{\mu}_k', \varSigma_k')}{\sum_{l=1}^K \pi_l' \mathcal{N}(\bm{x}_i|\bm{\mu}_l', \varSigma_l')}$ |
| M-Step | $\theta' = \operatorname{argmax}_{\theta} Q(\theta, \theta')$を計算 | $\pi_k', \bm{\mu}_k', \varSigma_k'$の更新(第1回の記事参照) |
さて,全3回にわたってEMアルゴリズムについて紹介した. EMアルゴリズムというと難しいイメージがあるが,なるべく噛み砕いて,丁寧に説明をしたつもりだ. 「ここがわからない...」みたいなのがあれば是非コメントしてください!
niltatsu
これなら分かるEMアルゴリズム②
前回は主に混合分布モデルによるEMアルゴリズムについて解説した. 計算は少々大変だが,思考の流れさえ把握できれば,その考え方は難しくないだろう. まだ読んでいない!という方は以下の記事を参照してください:
さて,前回はなるべく「潜在変数モデル」や「$Q$関数」などの用語を使用せずに混合分布モデルによるEMアルゴリズムを解説したが,やはりEMアルゴリズムの一般形を理解するには,これらの概念は非常に重要になってくる. そこで今回はこれらの概念,そして一般化したEMアルゴリズムについて解説する.
問題設定・潜在変数モデル
今回は混合分布モデル,さらには特定の分布を仮定しない場合のEMアルゴリズムについて紹介する. まず観測変数を$\bm{X}$とおき,モデルのパラメータを$\theta$とおく. いま,データ$\mathcal{D}$が与えられたとして,$\mathcal{D}$を用いて$p(\bm{X} | \theta)$の最尤推定を行うことを考える. この場合,解きたい最適化問題は以下のようになる: $$ \max_{\theta} \log p(\mathcal{D} | \theta) $$ これが解ければとてもハッピーなのだが,実際にこれが解けない場合を考える(混合分布モデルの場合を思い出して欲しい).
ここで突然だが,潜在変数$\bm{Z}$というものを導入する. 潜在変数とは,直接観測はされないが,モデルの中には実在する変数で,サンプル生成の背後にある状態・因果関係などを記述する際に用いられる. そして,この潜在変数を用いたモデルのことを潜在変数モデルと呼ぶ. 潜在変数モデルでは,$\theta$によって条件つけられた$\bm{X}, \bm{Z}$の同時分布$p(\bm{X}, \bm{Z}|\theta)$を考える. そして実際に観測されるのは$\bm{Z}$によって周辺化された確率分布$p(\bm{X} | \theta)$に従うサンプルであると考える. 式で言えば,以下のようになる: $$ p(\bm{X} | \theta) = \sum_{\bm{Z}} p(\bm{X}, \bm{Z}|\theta). $$ すると,上の最適化問題は以下のように置き換えることが可能になる: $$ \max_{\theta} \log p(\mathcal{D} | \theta) = \max_{\theta} \log \sum_{\bm{Z}} p(\mathcal{D}, \bm{Z}|\theta). $$ ゆえに,右辺の最適化を解くことが今回のゴールとなり,これを実現するアルゴリズムがEMアルゴリズムというわけだ. 以下では説明の便宜上,上の最適化問題を $$ \max_{\theta} \log p(\bm{X} | \theta) = \max_{\theta} \log \sum_{\bm{Z}} p(\bm{X}, \bm{Z}|\theta). \tag{1} $$ のように書く.
Jensenの不等式を用いた下界の導出
さて,前回のの記事をご覧になった読者はここで気づくはずだが,最適化問題(1)の右辺が$\log$関数の中に和が入っている形になっており,解くのが大変である. そこで前回同様Jensenの不等式により下界を求め,それを最大化することで間接的に元の対数尤度を最大化することを考える. 前回の記事では$q_k^{(n)}$を導入したが,今回は$q(\bm{Z})$を導入する. ただし,$q$は$\sum_{\bm{Z}} q(\bm{Z}) = 1$を満たすとする. すると,目的関数の下界として以下が求まる: $$ \begin{aligned} \log \sum_{\bm{Z}} p(\bm{X}, \bm{Z}|\theta) &= \log \sum_{\bm{Z}} q(\bm{Z}) \dfrac{p(\bm{X}, \bm{Z}|\theta)}{q(\bm{Z})} \\ &\geq \sum_{\bm{Z}} q(\bm{Z}) \log \dfrac{p(\bm{X}, \bm{Z}|\theta)}{q(\bm{Z})} \eqqcolon \mathcal{L}(q, \theta). \end{aligned} $$ ここで,1行目から2行目の不等式においてJensenの不等式を利用した. $\mathcal{L}(q, \theta)$は変分下限と呼ばれており,対数尤度の下界として理解していただければ良い.
変分下限と対数尤度の関係
上節で,対数尤度$\log p(\bm{X}|\theta)$の変分下限$\mathcal{L}(q, \theta)$を求めた. ここで気になる人は気になるかもしれないが,この両者の差は一体何だろうか? 実際に計算してみよう. $\sum_{\bm{Z}} q(\bm{Z}) = 1$であることに注意すると, $$ \begin{aligned} \log p(\bm{X}|\theta) - \mathcal{L}(q, \theta) &= \log p(\bm{X}|\theta) \sum_{\bm{Z}} q(\bm{Z}) - \sum_{\bm{Z}} q(\bm{Z}) \log \dfrac{p(\bm{X}, \bm{Z}|\theta)}{q(\bm{Z})} \\ &= \sum_{\bm{Z}} q(\bm{Z}) \log p(\bm{X}|\theta) - \sum_{\bm{Z}} q(\bm{Z}) \log \dfrac{p(\bm{Z}|\bm{X}, \theta) p(\bm{X}|\theta)}{q(\bm{Z})} \\ &= -\sum_{\bm{Z}} q(\bm{Z}) \log \dfrac{p(\bm{Z}|\bm{X}, \theta)}{q(\bm{Z})}\\ &= \mathcal{D}_{\mathrm{KL}} \Bigl( q(\bm{Z}) \Big| \Big| p(\bm{Z}|\bm{X}, \theta) \Bigr). \end{aligned} $$ ほうほう,対数尤度と変分下限の差はKLダイバージェンスなのか...! 実はこの後このKLダイバージェンスは大切な役割を果たす.
EMアルゴリズムの概略
さて,ここまでで混合分布モデルではなく,一般のモデルの場合でも使える変分下限を導出した. ここで一度EMアルゴリズムの概略を一回眺めてみよう.
EMアルゴリズム(一般形)
- 初期化: $\theta, q$を適当に初期化
- While 収束していない do:
- E-step: 現在の$\theta$を用いて$q$を計算
- M-step: 現在の$q$を用いて$\theta$を計算
前回の記事を読んでいただいた方は混合分布モデルの場合と照らし合わせて考えると分かりやすいかもしれない. このE-Step,M-Stepは一般の場合ではどのようにして計算できるのか,以下でそれを見ていきたいと思う.
E-Stepの計算
前回の記事で書いたが,混合正規分布モデルの場合は$\theta$を固定し,$\mathcal{L}(q, \theta)$の$q$について最大化,つまり「$q$について微分=0」の方程式を解けば良かった. では一般形の場合はどうすれば良いのか. ここで使用するのが変分下限と対数尤度の関係である: $$ \log p(\bm{X}|\theta) = \mathcal{L}(q, \theta) + \mathcal{D}_{\mathrm{KL}} \Bigl( q(\bm{Z}) \Big| \Big| p(\bm{Z}|\bm{X}, \theta) \Bigr). $$ $\theta$を$\theta'$に固定し,上の式とにらめっこして,$\mathcal{L}(q, \theta)$の$q$について最大化について考えると,以下の知見が得られる:
- $\log p(\bm{X}|\theta')$は$q$によらない関数 = $q$を動かしても左辺は変わらない
- この場合,「$\mathcal{L}(q, \theta')$の最大化 = $\mathcal{D}_{\mathrm{KL}} \Bigl( q(\bm{Z}) \Big| \Big| p(\bm{Z}|\bm{X}, \theta') \Bigr)$の最小化」
- KLダイバージェンスの非負性から,$\mathcal{D}_{\mathrm{KL}} \Bigl( q(\bm{Z}) \Big| \Big| p(\bm{Z}|\bm{X}, \theta') \Bigr)$の最小値は$0$で,最小値を達成するときの$q(\bm{Z}) = p(\bm{Z}|\bm{X}, \theta')$
ゆえに,結局$\mathcal{L}(q, \theta')$の$q$について最大化の最適解は$q(\bm{Z}) = p(\bm{Z}|\bm{X}, \theta')$となる. 前回の記事の場合E-Stepの計算をするために微分したりしたが,実は上のようにKLダイバージェンスを使用すればあっさりと解けてしまうのである.
M-Stepの計算
次にE-Stepで得られた$q$を用いて$\theta$について$\mathcal{L}(q, \theta)$を最大化する. まずE-Stepの結果を変分下限に適用すると, $$ \begin{aligned} \mathcal{L}(q, \theta) &= \sum_{\bm{Z}} q(\bm{Z}) \log \dfrac{p(\bm{X}, \bm{Z}|\theta)}{q(\bm{Z})} \\ &= \sum_{\bm{Z}} p(\bm{Z}|\bm{X}, \theta') \log \dfrac{p(\bm{X}, \bm{Z}|\theta)}{p(\bm{Z}|\bm{X}, \theta')} \\ &= \sum_{\bm{Z}} p(\bm{Z}|\bm{X}, \theta') \log p(\bm{X}, \bm{Z}|\theta) - \sum_{\bm{Z}} p(\bm{Z}|\bm{X}, \theta') \log p(\bm{Z}|\bm{X}, \theta') \\ &= Q(\theta, \theta') + \mathrm{const} \end{aligned} $$ となる. 3行目の第2項は$\theta$を含まないので,$\theta$についての最大化に際しては単なる定数である. 一方第1項は$\theta$が含まれるので,$\mathcal{L}(q, \theta)$の最大化は実質この項の最大化に等しい. この第1項は$Q$関数と呼ばれている. ゆえに,M-Stepですべき$\mathcal{L}(q, \theta)$の$\theta$についての最大化は, $$ \operatorname{argmax}_{\theta} Q(\theta, \theta') $$ と等価である.
一般のEMアルゴリズムのまとめ
さて,以上の知見をもとに一般の場合のEMアルゴリズムを再構成すると,以下のようになる:
EMアルゴリズム(一般形)
- 初期化: $\theta, q$を適当に初期化
- While 収束していない do:
- E-step: $q(\bm{Z}) = p(\bm{Z}|\bm{X}, \theta')$を計算
- M-step: $\theta' = \operatorname{argmax}_{\theta} Q(\theta, \theta')$を計算
実際にこれを図にすると以下の図のようになる.

やっていることとしては,$\log p(\bm{X} |\theta)$の最大値を求めるために,青線や緑線のような変分下限を考え,その下限の最大値を次のステップのパラメータとして使用する. これを繰り返すことで,徐々に$\log p(\bm{X} |\theta)$の最大値に近づけていく,という作戦である. このように上下限を利用することで最適値を達成する点を求めるアルゴリズムはたくさんあり,例えば近接勾配法などがある. 是非これを気に調べてもらえると良い.
まとめ
今回は特定のモデルを仮定せずに,一般の場合のEMアルゴリズムについて紹介した. なるべく分かりやすく紹介したつもりだが,この記事を読んでも初心者にはこの一般版EMアルゴリズムと混合分布モデルEMアルゴリズムの繋がりが見えないかもしれない. (長くなってしまったので)そこで次回はこの2者の関連と,さらには混合分布モデルにおけるスムージングについて紹介する.
niltatsu
これなら分かるEMアルゴリズム①
今回は主にEMアルゴリズムについて. 筆者が初めてEMアルゴリズムを見たのは学部3年の機械学習の授業の頃. そのときは教師無し学習の話からスタートし,まずは$k$-meansアルゴリズム. 「ふむふむ,クラスタ数を事前に決めといて,平均を近くのデータ点を使ってどんどん更新するのね,分かりやすい.」
そのままの流れでEMアルゴリズムへ. そこで難易度が急激アップ. 「潜在変数」「$Q$関数」「寄与率」などの単語が急にたくさん出てきて大混乱. しかも途中の計算が慣れないとそこそこ大変なので,結局何をやっているのかさっぱり.
しばらく経って,様々な場面でEMアルゴリズムを拝見し,自分なりに納得のいく説明の仕方ができたので,ここで書こうと思う. 個人的には,初心者にいきなり「潜在変数」や「$Q$関数」などの概念を出しても全く分からない原因になるだけだと思っている. これらの用語を使わなくても,EMアルゴリズムは説明可能である. なので,以下ではまずこれらの用語を用いない導出を行う(そのため,他の記事や本などと比較して,少々異なる理論構成になっているかも). ただし,いざ書いてみるとかなりの長さになるので,複数回に分けて紹介しようと思う. 今回は混合正規分布の最尤推定によるクラスタリング手法から.
問題設定
データ$\mathcal{D} = \{ \bm{x}_i \}_{i=1}^n \subset \mathbb{R}^d$が与えられたとして,これらを$K$個のまとまり(クラスタ)にクラスタリングすることを考える. 混合分布モデルでは,データの分布$p(\bm{x} | \Theta)$を以下のような形でモデリングする: $$ p(\bm{x} | \Theta) = \sum_{k=1} ^K \pi_k p(\bm{x} | \bm{\theta}_k). $$ ここで,$\pi_k$は$\sum_{k=1} ^K \pi_k = 1$を満たし,$\Theta = \{ \pi_1, \ldots, \pi_K, \bm{\theta}_1, \ldots, \bm{\theta}_K \}$とする. 特に,$p(\bm{x} | \bm{\theta}_k)$が正規分布,すなわち$p(\bm{x} | \bm{\theta}_k) = \mathcal{N} (\bm{x} | \bm{\mu}_k, \varSigma_k)$の場合,混合正規分布モデルと呼ばれる. 当たり前だが,この場合$\bm{\theta}_k = \{ \bm{\mu}_k, \varSigma_k \}$となる. 混合分布モデルの気持ちとしては...
- データの分布は$K$個のクラスタによって生成されており,$k$番目のクラスタの分布は$p(\bm{x} | \bm{\theta}_k)$.各クラスタがクラスに対応する多クラス分類問題で例えるなら,$p(\bm{x}|y=k)$に相当.
- $\pi_k$は混合係数と呼ばれ,各クラスタの「重み」のようなもの.各クラスタがクラスに対応する多クラス分類問題で例えるなら,$p(y=k)$に相当.
最終的なゴールとしては,$\Theta$の各パラメータを求まれば良い,ということになる. これを実行するためには最尤推定,すなわち,以下の最適化問題を$\Theta$について解けば良いということになる: $$ \max_{ \bf{1}^\top \bm{\pi} = 1} \sum_{i = 1}^n \log p(\bm{x}_i | \Theta) = \max_{ \bf{1}^\top \bm{\pi} = 1} \sum_{i = 1}^n \log \left( \sum_{k=1} ^K \pi_k p(\bm{x}_i | \bm{\theta}_k) \right). \tag{1} $$
ぶっちゃけ問題設定としてはこれ以上もこれ以下でもない. 何かしらの手段を用いて最適化問題(1)が解ければクラスタリング大成功である. しかし,世の中そんな甘くはない... 右辺を見て欲しい. $\log$関数の中に和が入っている. 「これが何だよ」というわけだが,想像してほしい. この最適化問題を解くためには,ラグランジュ乗数を導入し,ラグランジュ関数を微分して$0$を解けば良いわけだ. しかし$\log$関数の中に和があると,微分して得られる関数は分数関数で,分母に和が残る形になる. 更に言えば,$\pi_k$もしくは$\bm{\theta}_k$について微分したのにも関わらず,微分して得られる関数は$\pi_1, \ldots, \pi_K, \bm{\theta}_1, \ldots, \bm{\theta}_K$全部が絡み合った分数連立方程式になっているわけだ. こんなの解けっこない. つまり,この最適化問題を直接解くのを諦める他ない.
そこで考案されたのがEMアルゴリズムだ.
Jensenの不等式を用いた下界の導出
さて,最適化問題(1)を解きたいけど解けない. このような場合,良く用いられるのが「別の解きやすい関数を考え,それを解くことで間接的に元の問題を解く」という方法である. 今回の場合,$\log$関数の中に和があるのが難しさの元凶なので,これを崩せさえすれば良い. 「$\log$関数の中に和」の形に出くわしたときに役に立つのがJensenの不等式である.
Jensenの不等式
定理: (Jensenの不等式) $c_k$を$c_k \geq 0, \sum_{k=1}^K c_k = 1$を満たす実数とし,$x_k\ (k=1, \ldots, K)$を任意の実数とする.このとき,上に凸な関数$f$に対して,以下の不等式が成立する: $$ f \left( \sum_{k=1}^K c_k x_k \right) \geq \sum_{k=1}^K c_k f ( x_k ). \tag{2} $$ 等号成立条件は$x_1 = \cdots = x_K$である.
証明に関しては以下の図を見れば明らかであろう.
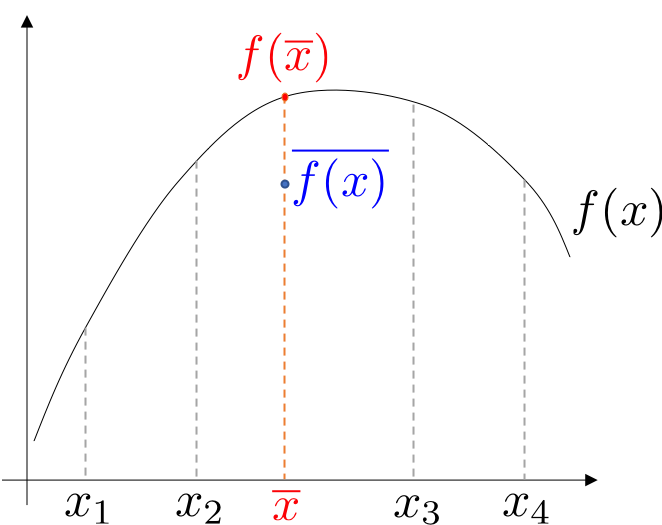
さて,このJensenの不等式を使うと何が良いのか. 不等式(2)における$f$を$\log$関数として考えると,左辺はまさしく最尤推定の最適化問題で現れる$\log$関数の中に和がある形になることが分かるだろう. つまり,「和の$\log$ $\geq$ $\log$の和」なので,「$\log$の和」が「和の$\log$」の下界を与える. 最適化問題(1)の下界を最大化することで,最適化問題(1)そのものも大きくしていこう,というのがEMアルゴリズムのアイデアである. さて以下では,対数尤度の式に対していかにしてJensenの不等式を適用していくのか見ていこう.
作戦1: $\pi_k$を$c_k$とみなす
まず容易に思いつくのが「$\pi_k$を$c_k$とみなす」という作戦である. これを実際にやってみると, $$ \sum_{i = 1}^n \log \left( \sum_{k=1} ^K \pi_k p(\bm{x}_i | \bm{\theta}_k) \right) \geq \sum_{i = 1}^n \sum_{k=1} ^K \pi_k \log p(\bm{x}_i | \bm{\theta}_k) $$ となる. いまやりたいことは対数尤度の下界の最大化なので,以下の最適化問題を解けば良いことになる: $$ \max_{\bf{1}^\top \bm{\pi} = 1} \sum_{i = 1}^n \sum_{k=1} ^K \pi_k \log p(\bm{x}_i | \bm{\theta}_k). $$ さて,これを実際に解いていこう. いまラグランジュ乗数$\alpha$を導入すると,ラグランジュ関数は以下のように書ける: $$ L(\Theta, \alpha, \mathcal{D}) = \sum_{i = 1}^n \sum_{k=1} ^K \pi_k \log p(\bm{x}_i | \bm{\theta}_k) + \alpha \left( \sum_{k=1}^K \pi_k - 1 \right). $$ 最適性条件から,$\bm{\theta}_k, \pi_k, \alpha$について微分すると,以下のようになる. $$ \begin{aligned}\tag{3} \dfrac{\partial}{\partial \bm{\theta}_k} L(\Theta, \alpha, \mathcal{D}) &= \sum_{i = 1}^n \pi_k \dfrac{\partial}{\partial \bm{\theta}_k} \log p(\bm{x}_i | \bm{\theta}_k) = 0, \\ \dfrac{\partial}{\partial \pi_k} L(\Theta, \alpha, \mathcal{D}) &= \sum_{i = 1}^n \log p(\bm{x}_i | \bm{\theta}_k) + \alpha = 0, \\ \dfrac{\partial}{\partial \alpha} L(\Theta, \alpha, \mathcal{D}) &= \sum_{k=1}^K \pi_k -1 = 0. \end{aligned} $$ さて,混合正規分布の場合,$p(\bm{x} | \bm{\theta}_k) = \mathcal{N} (\bm{x} | \bm{\mu}_k, \varSigma_k)$であるので,これを実際に代入すると, $$ \begin{aligned} \hat{\bm{\mu}}_k &= \dfrac{1}{n} \sum_{i=1}^n \bm{x}_i, \\ \hat{\varSigma}_k &= \dfrac{1}{n} \sum_{i=1}^n (\bm{x}_i - \hat{\bm{\mu}}_k) (\bm{x}_i - \hat{\bm{\mu}}_k)^\top, \\ \hat{\pi}_k &= \dfrac{1}{K}. \end{aligned} $$ あれれ〜?おかしいな... これって結局全部のクラスタで同じパラメータを共有しているから,「混合」正規分布になってなくない? てかただの1つの正規分布の最尤推定やん... ということでこの作戦は失敗...
作戦2: 新たな$q_k^{(i)}$を作り出す
さて,作戦1は失敗に終わった. 一回ここでその原因について反省してみよう. 方程式(3)を見ると,最適解が$k$に依存しないような形になってしまっている. $k$によらないということは,変な話,各クラスタに「個性」がないのである. ゆえに最適解が$k$に依存する形,つまり各々の最適解に「個性」を持たせれば良い. そこで新たな変数として,$q_k^{(i)}$を考え,以下のように「1をかける」: $$ \sum_{i = 1}^n \log \left( \sum_{k=1} ^K \pi_k p(\bm{x}_i | \bm{\theta}_k) \right) = \sum_{i = 1}^n \log \left( \sum_{k=1} ^K q_k^{(i)} \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right). $$ ただし「諸事情により」,$\sum_{k=1}^K q_k^{(i)} = 1$なる制約を設ける. 直感的にはこの制約がないと,$q_k^{(i)}$をそれぞれ無限大に大きくすればいくらでも目的関数が大きくなるので,最適化問題としての意味がなくなってしまう. さて,この右辺に対してJensenの不等式を適用すると, $$ \sum_{i = 1}^n \log \left( \sum_{k=1} ^K q_k^{(i)} \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right) \geq \sum_{i = 1}^n \sum_{k=1} ^K q_k^{(i)} \log \left( \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right) $$ という下界が得られる. よって最終的に私たちが解きたい最適化問題は以下のようになる: $$ \max_{\bf{1}^\top \bm{\pi}=1, \bf{1}^\top \bm{q}^{(i)} = 1} \sum_{i = 1}^n \sum_{k=1} ^K q_k^{(i)} \log \left( \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right). \tag{4} $$ 「この$q_k^{(i)}$を導入すると本当に$k$に依存する最適解が得られるの?」 この疑問については以下で解消しよう.
下界の最適化
ここからは最適化問題(4)を解いていく. この手の最適化問題は上の(3)式でやったように,ラグランジュ乗数を導入してラグランジュ関数の最適化に持ち込むのが定石である. ラグランジュ乗数$\alpha, \bm{\beta}$を導入すると, $$ \begin{aligned} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) = &\sum_{i=1}^n \sum_{k=1}^K q_k^{(i)} \log \left( \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right)\\ &+ \alpha \left( \sum_{k=1}^K \pi_k -1 \right) + \sum_{i=1}^n \beta_i \left( \sum_{k=1}^K q_k^{(i)} -1 \right) \end{aligned} $$ うーん,長い式になってしまった...が仕方がない. さて,ここからは少々大変な作業になるが,実際に$\bm{\theta}_k, \pi_k, \alpha, \beta_i, q_k^{(i)}$で微分していくと: $$ \begin{aligned} \tag{5} \dfrac{\partial}{\partial \bm{\theta}_k} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) &= \sum_{i=1}^n q_k^{(i)} \dfrac{\partial}{\partial \bm{\theta}_k} \log p(\bm{x}_i | \bm{\theta}_k) = 0, \\ \dfrac{\partial}{\partial \pi_k} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) &= \sum_{i=1}^n \dfrac{q_k^{(i)}}{\pi_k} + \alpha = 0, \\ \dfrac{\partial}{\partial \alpha} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) &= \sum_{k=1}^K \pi_k -1 = 0, \\ \dfrac{\partial}{\partial \beta_i} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) &= \sum_{k=1}^K q_k^{(i)} - 1 = 0, \\ \dfrac{\partial}{\partial q_k^{(i)}} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) &= \log \left( \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right) - 1 + \beta_i = 0, \end{aligned} $$ となる. さて,方程式(5)を眺めてみよう. うーん...どこから解き始めれば良いことか... まず結論から言おう. これはこのままでは解析的には解けない. 厄介な理由は$q_k^{(i)}$が5本の式中4本に現れていて,非常に複雑に絡み合っている点にある.
元々は最適化問題(1)が解きにくいからJensenの不等式とか使って苦労して別の最適化問題(4)を作ったのに,それがまた解けないとは何事じゃ!?w これはごもっともな意見だし,筆者もこれに悩まされた. ただ実は,元の最適化問題(1)は「ほぼ解けない」のだが,最適化問題(4)(つまり方程式(5))を解く手段はまだ残されている.
最適化の作戦
では方程式(5)をどのように解けば良いのか. もう一度言うが,方程式(5)が厄介なのは$q_k^{(i)}$がいたるところに現れているのが問題なのである. じゃあ,$q_k^{(i)}$を固定してしまえば良い. もう少し正確に言えば,
- $q_k^{(i)}$を既知にして$\Theta$について方程式(5)を解く
- $\Theta$を既知にして$q_k^{(i)}$について方程式(5)を解く
ようにする. $\Theta$と$q_k^{(i)}$のいずれか片方を固定してもう片方を解くことで,どんどん方程式の解に近づけようという作戦である. このように,片方の変数を固定してもう片方の変数について最適化するようなアルゴリズムを交互最適化アルゴリズムと呼ぶ. これは片方の変数orパラメータがもう片方の変数orパラメータに複雑に絡み合っている場合に有効な手法だ. では以下でそのこの交互最適化を実行していく.
$q_k^{(i)}$の最適化
まずは$\Theta$を固定して$q_k^{(i)}$について解く. これを実行するには方程式(5)の5本目の式に着目する(他の式は$q_k^{(i)}$についての和分になっているので解けない...). これを$q_k^{(i)}$について解くと, $$ \begin{aligned} \hat{q}_k^{(i)} = \exp(1-\beta_i) \pi_k p(\bm{x}_i | \bm{\theta}_k) \end{aligned} $$ が得られる. ここで方程式(5)の4本目の式を利用すれば, $$ \begin{aligned} \hat{q}_k^{(i)} = \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{\sum_{k'=1}^K \pi_{k'} p(\bm{x}_i | \bm{\theta}_{k'})} \end{aligned} $$ と求めることができる. さて,ここでこの式の意味について考えてみる. $K$クラスの多クラス分類問題の場合と照らし合わせると,$\pi_k = p(y=k)$,$p(\bm{x} | \bm{\theta}_k) = p(\bm{x}|y=k)$などと対応づけが可能である. ゆえにベイズの定理から, $$ \begin{aligned} \hat{q}_k^{(i)} = \dfrac{p(y=k) p(\bm{x}_i | y=k)}{\sum_{k'=1}^K p(y=k) p(\bm{x}_i | y=k')} = p(y=k|\bm{x}_i) \end{aligned} $$ が成立する. $q_k^{(i)}$は「$i$番目のデータが$k$番目のクラスタどのくらい寄与しているのか」を表しているので,寄与率と呼ばれる.
$\Theta$の最適化
さて,以上で得られた$q_k^{(i)}$を固定して次に$\Theta$について解く.
$\pi_k$の最適化
これは方程式(5)の2本目の式に着目する. これを$\pi_k$について解くと, $$ \begin{aligned} \hat{\pi}_k = - \dfrac{1}{\alpha} \sum_{i=1}^n q_k^{(i)} \end{aligned} $$ が得られる. ここで方程式(5)の3本目の式を利用すれば, $$ \begin{aligned} \hat{\pi}_k = \dfrac{1}{n} \sum_{i=1}^n q_k^{(i)} \end{aligned} $$ と求めることができる. さて,ここでこの式の意味について考えてみる. $K$クラスの多クラス分類問題の場合と照らし合わせると, $$ \begin{aligned} \hat{\pi}_k = \dfrac{1}{n} \sum_{i=1}^n q_k^{(i)} = \dfrac{1}{n} \sum_{i=1}^n p(y=k|\bm{x}_i) \simeq \int p(y=k|\bm{x}) p(\bm{x}) \mathrm{d} \bm{x} = p(y=k) \end{aligned} $$ となり,$\pi_k = p(y=k)$の直感とも合致する.
$\theta_k$の最適化
これは方程式(5)の1本目の式に着目する. 一般形の形だとここまでしか解けない. ただし,混合正規分布モデルの場合,$\mu_k$について解くと, $$ \begin{aligned} \hat{\bm{\mu}}_k = \dfrac{\sum_{i=1}^n q_k^{(i)} \bm{x}_i}{\sum_{i=1}^n q_k^{(i)}} \end{aligned} $$ と求めることができる. また,$\varSigma_k$について解くと, $$ \begin{aligned} \hat{\varSigma}_k = \dfrac{\sum_{i=1}^n q_k^{(i)} (\bm{x}_i - \hat{\bm{\mu}_k}) (\bm{x}_i - \hat{\bm{\mu}_k})^\top}{\sum_{i=1}^n q_k^{(i)}} \end{aligned} $$ が得られる. さて,ここでこれらの式の意味について考えてみる. $K$クラスの多クラス分類問題の場合と照らし合わせると, $$ \begin{aligned} \hat{\bm{\mu}}_k &= \dfrac{\sum_{i=1}^n q_k^{(i)} \bm{x}_i}{\sum_{i=1}^n q_k^{(i)}} = \dfrac{\dfrac{1}{n} \sum_{i=1}^n q_k^{(i)} \bm{x}_i}{\dfrac{1}{n} \sum_{i=1}^n q_k^{(i)}} \\ &\simeq \dfrac{\int \bm{x} p(y=k|\bm{x}) p(\bm{x}) \mathrm{d} \bm{x}}{p(y=k)} = \int \bm{x} p(\bm{x}|y=k) \mathrm{d} \bm{x} = \mathbb{E}_{p(\bm{X}|Y=k)} \left[ \bm{X} \right] \end{aligned} $$ となり,$\bm{\mu}_k = \mathbb{E}_{p(\bm{X}|Y=k)} \left[ \bm{X} \right]$の直感とも合致する. また$\varSigma_k$についても同様に計算すれば$\mathbb{E}_{p(\bm{X}|Y=k)} \left[ (\bm{X}-\bm{\mu}_k) (\bm{X}-\bm{\mu}_k)^\top \right]$のようになる.
$q_k^{(i)}$を導入すると本当に$k$に依存する最適解が得られるの?
さてここで$q_k^{(i)}$を導入した際に生じた上記の疑問について答えよう. ずばり,答えはyesである. 実際に上の$\bm{\mu}_k, \varSigma_k, \pi_k$の結果を見て欲しい. $q_k^{(i)}$がはさまってことによって,($\bm{q}_k$が互いに異なれば)当然ながら$\bm{\mu}_k, \varSigma_k, \pi_k$の推定値も異なるのである. つまり,この$q_k^{(i)}$はいわば「個性」をもたらす役割を果たしているのである.
アルゴリズムのまとめ
最後に一回このアルゴリズムについてまとめていこう. 思考の流れとしては以下のようになる:
こう考えるとアルゴリズムの導出の思考過程も非常に分かりやすいのではないのでしょうか.
さて,最後に以下に混合分布モデルのアルゴリズムについてまとめる.
EMアルゴリズム(混合分布モデル)
- 初期化: $\Theta, \bm{q}$を適当に初期化
- While 収束していない do:
- 現在の$\Theta$を用いて$\bm{q}$を計算
- 現在の$\bm{q}$を用いて$\Theta$を計算
次回予告
さて,今回は主にEMアルゴリズムの最も基本的な部分について解説した. お分かりいただけただろうか... ただ今回お見せしたのは,EMアルゴリズムのほんの氷山の一角である. 次回はEMアルゴリズムのより詳細な一般論について述べる.
niltatsu
就活して思ったこと
今回はアカデミックそっちのけで去年の就活体験談を書いていきたいと思う. 筆者はちょうど1年前から就活を始め,半年前に無事第一志望の外資金融の企業からオファーを頂いた. 今回は就活を通して自分が思ったこと・考えたことについて書いていきたいと思う.
まずは就活の感想を!
まず個人的な就活の感想は「楽しかった」である. 就活と言うと「辛い」「しんどい」という意見が多い気がする. ただ筆者はそうは全く思わない. もちろん,上位志望の企業からオファーをもらったから楽しい部分があるのは否めない. ただ,筆者はそういうオファーをいただく前から楽しいと感じていた. 自分なりにその原因について分析してみた.
楽しかった理由1: 新たな友達ができた
まずこれは筆者の中で真っ先に思いついた理由なのだが,やはり新たな友達を作るのは楽しい. 就活を通して友達を得るチャンスはたくさんある. インターン・面接会場・ウェブテスト会場など. そこで知り合える人のバックグラウンドは本当に様々. 今までの大学生活・大学院生活で知り合える人はやはりかなりの偏りがあることを実感する. 筆者はずっと理系の世界で生きてきたこともあり,どうしても「理系的な」バックボーンを持つ人としか接することがなかった. しかし就活すると多種多様な人と出会えるので,良い意味で視野を広がる.
例えば筆者が会った中では大学で起業している人や,株の投資を行なっている人. コンサルをしている人や世界一周した人. 今まで理系の社会で生きてるとなかなか出会わない人たちだ. 彼ら彼女らは筆者に「ビジネス精神」「遊ぶ精神」という自分の中での新たな「文化」を開花させた. もちろん,一緒に飲んだり一緒に遊べる仲間ができたのも最高だ.
楽しかった理由2: 「ライアーゲーム」的な刺激
突然「お!?」と思うかもしれない. ライアーゲーム!? そう!あのライアーゲーム! 筆者が最も好きなテレビドラマの一つである. プレイヤーが一堂に会し,言い渡されるゲームを元にマネーの奪い合いを行う. ルールさえ破らなければ,騙すもOK,裏切るもOK,脅すもOK,協力もOK. そこにあるのは剥き出しの人間の欲望の争い. 敗者には微塵の容赦もない恐ろしいゲームだ.
ズバリ言おう. 就活はライアーゲームである,と. プレイヤーは就活で出会った人たち全員. そこには就活でできた友達も,仲良くなった社員さんも含む. ゲームとは採用選考であり,全プレイヤーは自らの利潤を最大化するための行動を行う. そこには情けも容赦もない.
ライアーゲームで大切なのは2点あると筆者は考えている.
- 騙されないこと
- 良き仲間を作ること
まず1点目の騙されないことについてだが,これは会社にも就活生にもだ. 会社は説明会やインターンなどを通して自分たちの会社の良いところばかりを見せてくる. しかし何も不満のない会社など存在しない. そこを見極めずに万が一にも会社に入ってしまっては,ただの不幸である. また就活生も時には騙しにくる. 今やインターネット時代. 就活に関する情報なども掲示板などの形でネット上に流通している. しかしそこにあるのは真実とは限らず,他の就活生を貶めるための情報だって存在する. そこで大切になってくるのが2点目の良き仲間を作ることである. 仲間は良き情報共有者である. 自分の知っていること,そして自分の仲間の情報などと照らし合わせて真の情報を引き出すのが大切である.
この情報戦・ライアーゲーム的な部分. 嫌いな人も多いだろう. しかし筆者は非常に楽しめた. 自分で考え,自分で情報を操り,そして自分で成功を掴み取るのは普段の生活にはできない刺激的な体験だからだ. さらに言おう. このライアーゲームを楽しめた人が就活で勝利すると.
就活の際に気にすべきこと
身だしなみ
最初は筆者は身だしなみなんかどうでも良いだろうなと考えていたが,やはり就活を通してこれは大切なファクターなのだと確信した. 見た目は9割だと巷で言われているが,実際集団面接で身だしなみが微妙な人がいると,就活生側から見ても印象が悪い. ではどうすれば良いのか? 自分は男子なのであくまで男子側の話をすると(女子は実はほとんど身だしなみクリアしてると筆者は思っているので今回は略す),
- 髪の毛を整える
- スーツはパリッと着こなす
- 汗っぽい印象をいだかせない
である. まず1点目に関して,別に髪の毛をギトギトにワックス漬けにする必要はないと思う. 筆者も必要最低限のワックスしか就活時代つけていない(友達からはワックスつけたの?と言われるほど). しかし個人的に大切なのは,最低限寝癖を直すこと,そして最低限髪の毛を整えることだと思っている. 実際に面接会場に行くと,初期の方は寝癖のある人がいるのだが,選考が進むにつれてその数はどんどん減って行き,最終的には絶滅している. これはその身だしなみの現実を物語っている気がする.
またスーツに関してもやはり着こなしている人の方が随分仕事ができそうに見えるし,そのような人と仕事したいなと素直に思う. そして最後の汗っぽい印象だが,就活は夏に行われたりする. そのときに面接室に汗だくに入るとどうだろうか. うーん. 臭い,暑い,どっか行って欲しい...って素直に思う. 筆者はいつも面接の最低限30分前には会社近くのカフェなどに入って,汗を引かせてから会社に出向くようにした.
情報のアップデート
就活の情報は全て突然だし,早いもん勝ちである. そもそも知るのが遅れたら論外. また会社説明会ありますよ〜と告知されても,放置して2日後に申し込もうとすると,もうすでに定員になりました...と言われたことが何回もある. 面接も同じだが,数時間遅れただけで,希望の時間枠がすでに埋まっていることも多々あった. 上でも書いたが就活はぶっちゃけ情報戦であり,そこをいかに漏れなく処理できるかが勝負になってくる. そこは適宜社員さんや自分の就活仲間に聞いて,情報をアップデートすることが非常に大切である.
自己分析
自己分析なんかなんとかなると思っているそこのあなた! 面接なんかその場のノリでなんとかなると思っているそこの君! 筆者も正直初期の初期はそんな一人でした. しかし実際に就活を始めると,そんな甘っちょろい考えでは通用しないことを実感した.
筆者は外資金融業界を受けていたのだが,平均一社当たり10時間近くの面接をされた. 10時間も聞くことあるの?と思うかもしれないが,案外聞かれることはたくさんある. 「自己紹介」「自己PR」などのオーソドックスな質問から,「自分の嫌いなこと」「世の中に対して不満に思うこと」とかの突拍子も無い質問など,自分の人生観が様々な角度から切りこまれた. 自己分析などできなかった頃は,オーソドックスな質問に関してはなんとなく答えられ,突拍子も無い質問に関してはつまる....ようなことが日常茶飯事で,実際に面接で落とされたことが多々あった. しかし実際に自己分析をすると,初見の質問に対しても自分なりの答えを出せるようになったし,さらにオーソドックスな質問に対する答えも厚みをました.
さらに自己分析をして得したなと思ったのは面接中の余裕である. 自己分析をすると,同じ質問に対しても答えの選択肢が増え,面接官の人を見て適切な選択肢を答えることができるようになる. 例えば面接官が元体育会系の人だと分かれば,筆者は自己PRでなるべくサークルで頑張ったことを熱く語るようにしたし,相手が理系出身と分かれば,自己PRでは数学や情報系の話を多めに入れたりする. これは,自己分析をしなければ身につかなかったことだと言える.
就活の際に気にしなくても良いこと
無茶な演技・無意味な媚び
これをやる人は本当に多い. 筆者はインターンや会社の説明会などで,「質問ありますか?」と聞かれた際,必死に手を挙げ質問をして,自分の意識の高さをアピールしてくる就活生を見ては辟易とする. 日本の大学の講義で教授が「質問ありますか?」と聞いても誰一人も反応しないのに,就活になると過半数が手を挙げる. しかも質問が自体も意味不明・支離滅裂だったりする. 別に相手の社員さんも手を挙げてる人をいちいち覚えている訳でも無いのに. また,就活ノートを取り出して,背筋ピンと伸ばして,熱心にメモ取ってる光景も個人的には異様な光景に思える.
「真面目そう」「意識高そう」な演出をその場しのぎでやっても,結局会社に入るとすぐにバレる. なんなら面接するだけで無知であることが簡単にバレる.
ちなみにそんな無理な演技などをしなくても,内定は十分もらえる. 筆者もそうだし,内定先の同期で無理に媚びて内定した人など一人もいない. なぜなら社員さんも分かっているからである. 社員さんは一人一人みんな元は就活生. そういう現状を自分たちでも痛いほど分かっているのである. だからこそ,無闇に自分を良く見せようとする人には冷たい目線を送るし,選考で落としたりする.
常にありのままの自分をさらけ出すこと. これがもっとも重要なポイントだと思っている.
まとめ
今回は主に就活を通して思ったこと・そして感想について書いた. この記事は別に就活必勝書だとは言わないが,就活生の参考になればと思う.
niltatsu
機械学習概観 ~その③ 数値計算論編~
さて,機械学習概観,いよいよ最終回. 前回までの2回はそれぞれ学習フレームワーク論,そしてモデリング論に関して議論してきた. しかし問題設定とモデルを好き勝手に決めても,そこに莫大な計算コストがかかったしまっては良いアルゴリズムとは言えない. 故に問題設定とモデリングは数値計算の下支えがあってこそだとも言える. 今回はそのような数値計算部分について紹介していきたいと考えている. ここで,「学習フレームワーク論?モデリング論?」となっている方は以下の2記事を読んでいただきたい.
数値計算論
数値計算でのゴールは「いかに精度をなるべく落とさずに,少ない計算量を達成するか」だと言える. 以下ではそのような枠組みや,先人たちが計算量を落とすためにしてきた工夫などについて見ていく.
行列計算
まず数値計算において最も基本的な部分の一つである行列計算について説明する.
逆行列計算
逆行列の計算は最小二乗回帰などでも使用される行列計算の手法の一つである. しかし逆行列の計算は行列サイズ$n$に対して$\mathrm{O}(n^3)$の計算量がかかり,非常に大変である. この逆行列の計算をいかに回避or工夫するかが非常に大切になってくる.
この計算の工夫に関して2つほど論文を紹介する. まず1つ目は非定常状態下での密度比推定に関する論文*1である. この論文中のモデル選択の部分で,一つ抜き交差確認法(LOOCV)を用いているのだが,愚直にこれを実行しようとすると,データ数$n$に対して,
ので,モデル選択を含めた計算量として$\mathrm{O}(n^4)$かかってしまい,非常に遅い. そこで,こちらの論文では以下のSherman-Woodbury-Morrisonの公式を用いて計算量を削減している:
$$ \begin{aligned} (A + \bm{b} \bm{c}^\top )^{-1} = A^{-1} - \frac{A^{-1} \bm{b} \bm{c}^\top A^{-1}}{1 + \bm{c}^\top A^{-1} \bm{b}}. \end{aligned} $$
これを利用すると,逆行列の計算を1回のみ行うことでLOOCVの計算を行うことが可能になる. つまり,モデル選択を含めた計算量は$\mathrm{O}(n^3)$で済むということになる.
2つ目はカーネル法の計算量を抑えた論文*2だ. 例えば最小二乗回帰などではカーネル行列の逆行列などが必要になるが,この行列のサイズはデータ点の数に比例する. つまり,カーネル法は大規模なデータだと半端ない計算時間がかかってしまう. こちらの論文は,この問題をNyström methodと呼ばれる手法で解消しようとした. ざっくり言ってしまえば,全てのデータ点を使ってカーネル行列を再現するのではなく,ごく少量のデータのみを使ってカーネル行列を精度よく近似しよう,というアイデアである. 詳細は論文を本体を読んでいただきたい.
ヘッセ行列の計算
ヘッセ行列は特にモデル自体のバリアンス解析や,モデルの解釈性などを見る際に良く使用されるものである:
$$ \begin{aligned} H(f)(\bm{x}) = \nabla^2_\bm{x} f(\bm{x}). \end{aligned} $$
このヘッセ行列の計算も非常に大変で,特にディープモデルなど,パラメータ数が尋常じゃなく多いモデルなどを使用すると,とてつもない計算コストが発生してしまう.
しかし現実問題,ヘッセ行列単体が必要なケースはほぼなく,ヘッセ行列とベクトルの積を計算したい場合がほとんどである:
$$ \begin{aligned} H\bm{v} = \nabla_\bm{x} \Bigl[ (\nabla_\bm{x} f(\bm{x}))^\top \bm{v} \Bigr]. \end{aligned} $$
この場合,クリロフ法と呼ばれる手法を用いてヘッセ行列とベクトルの積を効率良く計算することが可能になる.
ICML2017のベストペーパー*3を紹介する. この論文では,影響関数と呼ばれる量を計算するのだが,その計算にはヘッセ行列の逆行列が必要になる(いかにもやばそう...). 愚直に計算しようとすると,データ数$n$,パラメータ数$d$に対し,ヘッセ行列の逆行列は$\mathrm{O}(nd^2 + d^3)$の計算量が必要になり,さらにこれを全てのデータ点ごとに計算するので,合計$\mathrm{O}(n^2 d^2 + nd^3)$の計算量が必要になる. この論文のすごいところは,この大変な計算をなんと合計$\mathrm{O}(nd)$の計算量まで落とした点にある. 詳細は書かないが,その工夫として共役勾配法などを用いているらしい.
固有値計算
固有値計算も機械学習でよく使用されるもので,例えば主成分分析(PCA)でも使用される. その計算コストは行列サイズ$n$に対して$\mathrm{O}(n^3)$であり,逆行列の計算同様大変重い. なので,これもいかに回避or工夫するかが非常に大切になってくる.
ベイズ推定における計算
ベイズ推定は機械学習で良く使用される手法の一つである(残念ながら筆者は頻度論者なので,ベイズに対する理解は浅い.もし間違いなどがあれば容赦なくご指摘ください...). 個人的な意見として,「ベイズは正直常に計算と格闘しているな...」と思っている(ベイズの方々ごめんなさい).
例えばベイズ推定ではしばしば以下の予測分布を計算する必要がある:
$$ \begin{aligned} p(x | \mathcal{D}) = \int p(x | \theta) p(\theta | \mathcal{D}) \mathrm{d} \theta. \end{aligned} $$
ここで,$\mathcal{D} = \lbrace x_1, \ldots, x_n \rbrace$である. この積分,書くのは簡単だが,計算は地獄のように難しい. 正直,ベイズの方々はこの積分の計算をするために並々ならぬ努力をしている. 以下では,その計算方法について紹介する.
モンテカルロ法 (Monte-Carlo Method)
モンテカルロ法では,積分するのを諦め,その代わりにサンプリングを行うことで積分の近似を求める:
$$ \begin{aligned} p(x | \mathcal{D}) = \int p(x | \theta) & p(\theta | \mathcal{D}) \mathrm{d} \theta \simeq \frac{1}{T} \sum_{t=1}^T p(x | \theta_t), \\ & \theta_t \sim p(\theta | \mathcal{D}). \end{aligned} $$
つまり,十分大きな$T$(サンプリング数)をとれば,積分の良い近似が得られるということである. その$\theta_t$をどのようにして得るのかがこの手法のミソだと言える. 実際この手法を用いると,比較的高い精度で積分を計算できる(らしい). 代表的なサンプリング手法としては:
- マルコフ連鎖モンテカルロ法(MCMC)
- ギブズサンプリング法(Gibbs Sampling) (これはMCMCのうちに入っている?)
- 粒子フィルタ
などがある.
変分近似 (Variational Inference)
上記のモンテカルロ法は確かに複雑な積分の計算を克服できる. しかも比較的高い精度で. しかし,それでもかなりの計算時間がかかるらしい. そこで精度を少し落としても良いので,なんとかして計算時間を落とせないか. それがこの変分近似である.
以下では事後分布$p(\theta | \mathcal{D})$を求めることを念頭に考える. 変分近似では,以下のように別の関数$q$を用いて事後分布を近似する:
$$ \begin{aligned} q(\theta) \simeq p(\theta | \mathcal{D}). \end{aligned} $$
この2つの分布をなるべく同じのものにしたいので,分布間の距離,例えばKLダイバージェンスを取り,その最小値を求める,というのが変分近似の考え方になる:
$$ \begin{aligned} \min_q \mathcal{D}_{\mathrm{KL}} \Bigl( q(\theta) \Big| \Big| p(\theta | \mathcal{D}) \Bigr) = \min_q \int q(\theta) \log \frac{q(\theta)}{p(\theta | \mathcal{D})} \mathrm{d} \theta. \end{aligned} $$
実際,変分近似を使うと,モンテカルロ法よりも早く積分を計算できる(らしい). しかし,精度はあまり保証されない(らしい). 直感的には,モンテカルロ法では,「本当の分布からサンプリング」しているので,精度が高く,変分近似は,別の関数を使って近似しているので,その近似がずれた場合は精度が低くなる. この精度と計算時間に関するトレードオフは実に面白い.
最適化計算
さて,数値計算の部分で最も大切なのがこの最適化計算だろう. 最適化計算に関しては「離散か連続か」「凸か非凸か」で分けることができる.
離散vs連続
- 連続最適化: 制約領域が$\mathbb{R}^n$の部分集合の最適化問題(機械学習の最適化問題のうち,体感ベースで90%は連続最適化)
- 離散最適化: 制約領域が$\mathbb{Z}^n$の部分集合の最適化問題(機械学習の最適化問題のうち,体感ベースで10%は離散最適化)
凸vs非凸
- 凸計画: 最小化すべき目的関数が凸関数であり,さらに実行可能領域が凸集合であるような最適化問題
- 非凸計画: 上記以外の最適化問題.すなわち,目的関数が非凸 or 実行可能領域が非凸集合であるような最適化問題
| 凸計画 | 非凸計画 | |
|---|---|---|
| 連続最適化 | 比較的簡単 | 難しい(ディープモデルなど) |
| 離散最適化 | 難しい(劣モジュラ関数最適化など) | 超難しい(NP困難な問題多数) |
最適化問題に関するカテゴリーに関するまとめの表は以上のようになる.
まず連続最適化と離散最適化についてだが,一般的に連続最適化に比べて離散最適化の方が難しい. またほとんどの機械学習の問題は連続最適化問題によって定式化される. しかし,これは離散最適化が全く使われないというわけではない. 実際は能動学習や,グラフ系の話で離散最適化のフレームワークが使われたりする. また,分類問題の序盤に出てくる01-リスクの最小化は実は組み合わせ最適化になっているので,これまた離散最適化だったりする.
次に凸計画と非凸計画について. 凸計画の嬉しいポイントは「局所的最適解$=$大域的最適解」である点で,勾配降下法などを用いて局所的最適解に辿り着けさえすれば,そこが自分たちが望む解になっている. かたや非凸計画の場合は「局所的最適解$\neq$大域的最適解」なので,局所最適解に陥り,本当に欲しい大域的最適解に辿り着けない. そういう意味で,凸計画に定式化してしまえば嬉しいことは多いように思える.

ただし,案外そのような単純な話ではない. 例えば分類手法の一つであるSVMは二次凸錐計画問題と呼ばれる最適化問題によって定式化され,これは凸計画である. しかし計算量は$\mathrm{O}(n^2 d)$であると言われており,ビッグデータを積極的に扱う最近の傾向にはそぐわない. かたや非凸計画であることの多いディープラーニングでよく使われるSGDと呼ばれる最適化手法は,データ数にほぼ依存しない計算量で比較的実用的な局所解を探してくれる. よって,アルゴリズムを設計する段階で「どのような最適化問題に落とし込むか」「何を重視するのか(大域最適解を見つけたいのかor計算時間を早くしたいのかなど)」をしっかり考えなければならない.
まとめ
今回は数値計算論全般に関する論点を概説した. ベイズ推定の話をここ数値計算のところに含めるべきかかなり悩んだが,「こういう区分の仕方もあるよ」というつもりで今回の話に含めた. この数値計算はいわば機械学習の根幹をなしており,機械学習研究者ならば避けて通れない部分と言えるだろう.
さて,以上3回を通して主に機械学習のバックボーンである3要素「学習フレームワーク論」「モデリング論」「数値計算論」について見てきた. 機械学習研究者やデータサイエンティストの方々はこの3要素のうち,自分たちがどこの部分をやっているのか把握すると良いのかもしれない. また初心者の方々はこの3要素をまず見てから勉強すると,今勉強していることやこれから勉強することのイメージが湧くかもしれない.
この3回の記事が機械学習に携わる全員の指南書になることを心の底から切に願う.
niltatsu
*1:Takafumi Kanamori, Shohei Hido, and Masashi Sugiyama. "Efficient direct density ratio estimation for non-stationarity adaptation and outlier detection." Advances in neural information processing systems. 2009.
*2:Christopher KI Williams, and Matthias Seeger. "Using the Nyström method to speed up kernel machines." Advances in neural information processing systems. 2001.
*3:Pan Wei Koh and Percy Liang. "Understanding black-box predictions via influence functions." In Proceedings of the International Conference on Machine Learning. 2017.
機械学習概観 ~その② モデリング論編~
さて,機械学習概観第2回. 前回は機械学習の3要素のうち,主に学習フレームワーク論,すなわち,どのような問題設定があるのかについて紹介した. ランキングなどのあまりお目にかからない問題設定なども紹介し,機械学習という分野の守備範囲の広さについてお分かり頂けたと思う. なお,「機械学習の3要素?学習フレームワーク論?」という方は以下の記事をまず読んでいただきたい.
さて,第2回は主にモデリング論についての紹介となる.
モデリング論
前回の教師有り学習での話を思い出していただきたい. 教師有り学習では,$f(\bm{x}) \simeq y$となるような$f$を求めることがゴールであると書いた. ところが写像$f$を見つけると言っても,$f$の自由度は非常に高く,あらゆる$f$を試すのは海の中にある針を一本見つけるのと同じくらい難しい.
そこで良く行われるのがモデリングで,$f$として,候補を絞ってしまうのである(この候補の集団をモデルと呼ぶ). そしてそのように候補を絞った場合に,どのような性質があるのかを研究するのがこのモデリング論である.
機械学習で良く使われるモデル
まずは機械学習でよく使用されるモデルに関して紹介する. ここで紹介するモデルはほんの一部で,さらに前回紹介した問題設定によっても使用されるモデルは様々. なのでより詳しいモデルなどについては各自調べると良い.
線形モデル (Linear Model)
以下では$\bm{x} \in \mathbb{R}^d$と,入力データは$d$次元のベクトルであると考える. 線形モデルは機械学習で最も使われているモデルの一つであり,以下のように定義される: $$ f_{\mathbf{\theta}} (\bm{x}) = \sum_{j=1}^b \theta_j \phi_j (\bm{x}). $$ ここで,$\theta_j$をパラメータと呼び,$\phi_j$のことを基底関数と呼ぶ. 基底関数については以下のような例($d=1$の場合)がある:
また,$b=d$,$\phi_j (\bm{x}) = x_j$の場合は,$d$次元の実数空間内の超平面に対応し,SVMなどの手法では,この超平面から議論がスタートすることが多い.
カーネルモデル (Kernel Model)
今手元に訓練標本$\bm{x}_i \ (i = 1,2, \ldots, n)$がある場合,以下で定義されるモデルをカーネルモデルと呼ぶ: $$ f_{\bm{\theta}} (\bm{x}) = \sum_{i=1}^{n} \theta_i K(\bm{x}, \bm{x}_i). $$ カーネルモデルのパラメータ数は$n$であり,入力次元$d$に依存しない. また,パラメータに対して線形なので,カーネルモデルは線形モデルの特殊な場合として考えることができる. しかし,パラメータ数が訓練標本数に依存するため,通常の線形モデルとは数学的な性質が異なることに注意. カーネルモデルで最も良く使用されるのが以下のガウシアンカーネルである: $$ K(\bm{x}, \bm{c}) = \exp \left( \frac{|| \bm{x} - \bm{c} ||^2}{2h^2} \right). $$
ディープモデル (Deep Model)
ディープモデルとは,以下の図のようなモデルで,人間や動物の脳神経回路を基にしたモデルである. ざっくり言ってしまえば,「どんどん層やパラメータを増やした多層構造をもつモデル」と言える. 下図では中間層が1層のみしかないが,最近のディープモデルは何百層も何千層もあり,非常に複雑なものになっている.

近年良く言われるディープラーニング(深層学習)というのは,このディープモデルを用いた学習方法全般を指す. つまり,ティープラーニング(深層学習)と呼ばれるものは,あくまでも機械学習の中でもモデルの話にすぎず,機械学習の中での一部にすぎないのである. ただしディープモデルはそのあまりもの柔軟さゆえ,まだ未知の部分が多く(実際数学的,理論的にも未知のことがほとんど),また最近の人気ぶりから,今やほとんどのモデルの研究に関する論文はディープモデルが対象である.
決定木モデル (Decision Tree Model)
決定木モデルとは,以下の図のような樹形のモデルである.
端的に言えば,段階的にデータを分割していき、木のような分析結果を出力するものと考えていただければ良い.

ディープモデルとは異なり,決定木モデルは解釈が容易で,また前処理も少なく済むので非常に人気のあるモデルであると言える.
モデル選択 (Model Selection)
モデルにはパラメータが存在し,そのパラメータの数をどのように決めるかは機械学習における重要な問題である. パラメータ数の決定,さらにはモデルそのものの選定に関する問題はモデル選択と呼ばれている. 一般的に,モデル選択,特にパラメータ数の決定に関して以下の事実が知られている:
- パラメータ数は少ないと情報不足により予測精度は悪くなる
- パラメータ数は多いと過学習が起こってしまい予測精度が悪くなる
ゆえに,なるべく必要十分な数の変数で予測した方が良いということであり,その「本当に必要な変数」を探すための学問がモデル選択だと言える. 以下では代表的なモデル選択方法について紹介する.
検定によるモデル選択
検定によるモデル選択では,ある変数が入っているモデルAとその変数が入っていないモデルBとを比較する.
- 当てはまりの差が「誤差の範囲内」であるならば,変数が少ない方のモデルBを採択
- 誤差の範囲内とは言えないのならば,変数が多い方のモデルAを採択
というようなモデル選択方法である.
情報量規準によるモデル選択
実用上は,検定よりも情報量規準によるモデル選択方法が多く使われる. 情報量規準とは,統計モデルの良さを評価するための指標であり,一般的に情報量規準が小さいものが最良のモデルとして選ばれる. 代表的な情報量規準としては以下のようなものがある:
- 赤池情報量規準(AIC): $- 2\log p(x^n; \hat{\theta}(x^n), k) + 2k$
- ベイズ情報量規準(BIC): $- \log p(x^n; \hat{\theta}(x^n), k) + \frac{k}{2} \log N$
- 最小記述長規準(MDL): $- \log p(x^n; \hat{\theta}(x^n), k) + \log \sum_{x^n} p(x^n; \hat{\theta}(x^n), k)$
バイアスとバリアンス (Bias and Variance)
モデリング周りの話で切り離せないのがバイアス(Bias)とバリアンス(Variance)の話である. まずバイアスとは「モデル精度の悪さ」もしくは「現在のモデルと真のモデルとのズレ」を意味する. 一方バリアンスとは「モデル作製の不安定さ」もしくは「再現性の悪さ」を意味する. このバイアスとバリアンスにはトレードオフの関係がある:
- モデルが単純(線形モデルなど)
- 性能は良くないが、教師データに対して安定
- 高バイアス・低バリアンス
- モデルが複雑(ディープモデルなど)
- 性能は良いが、教師データに対して不安定(過学習など)
- 低バイアス・高バリアンス
これを表しているのが以下の図である.
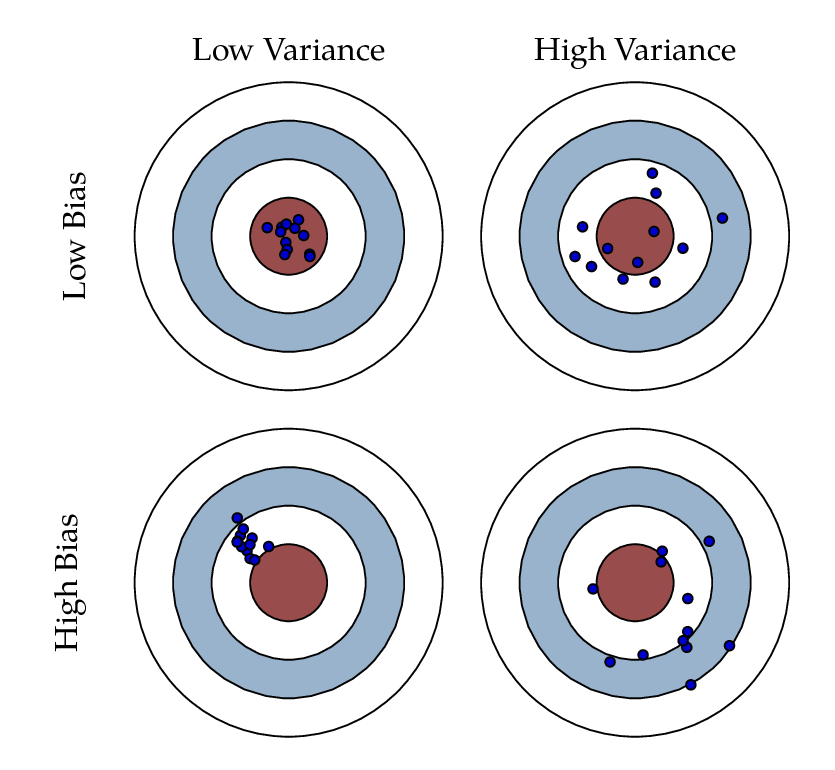
よくバイアス・バリアンストレードオフでは,二乗損失が例として使用される. これは,二乗損失を使用した場合は解析的に非常に綺麗な形でバイアスとバリアンスのトレードオフが見えるからである. 実はあまり知られていないが,分類問題で使用される0-1損失でもこのバイアス・バリアンストレードオフを見ることができる*1.
このバイアス・バリアンスの和を最小にするようにモデルを選択する必要がある(下図参照).これをコントロールするために導入されたのが以下に説明する正則化である.

正則化 (Regularization)
正則化の話をこのモデリング論の部分ですべきか否かは賛否両論だろうが,筆者は正則化はモデリングの部分と切って離せない関係だと考えているので,ここで紹介したいと思う.
一般的に,経験損失のみを最小化して得られる学習器は過学習のため汎化誤差は小さくならない. そこであえて平滑化を行う罰則項と経験損失の和を最小化することで汎化誤差を小さくさせる. 以上のような処理のことを正則化と呼び,罰則項$\lambda \Omega(\bm{\theta})$のことを正則化項と呼ぶ. $\Omega(\cdot)$の関数形によって様々な正則化が存在する:
- L2正則化(リッジ正則化):
- $\Omega(\bm{\theta}) = || \bm{\theta} ||_2^2$
- 最も普遍的に使用されている正則化
- L1正則化(LASSO):
- $\Omega(\bm{\theta}) = || \bm{\theta} ||_1$
- 学習結果を疎にする.特徴量選択の際にも使われる
- L0正則化:
- $\Omega(\bm{\theta}) = || \bm{\theta} ||_0$
- 学習結果を疎にする.特徴量選択の際にも使われるが計算コスト大
- Elastic Net:
またディープモデルでは,以上の正則化の他に,ディープモデルならではの正則化が使用される.
- ドロップアウト: 活性化関数の出力を一定の割合で$0$にする手法.情報の伝達をあえて断ち切り、少数の情報だけで学習することで過学習を防ぐ
- バッチ正規化: 各層ごとに標準化を行う手法
- ノイズ混入: ニューラルネットを学習させる際に,わざと入力データにランダムにノイズを混入させる手法
まとめ
今回は機械学習の3要素の内,主にモデリング論についての概要を与えた. ディープモデルの研究は今や機械学習研究の花形であり,またモデル選択や正則化なども機械学習の中で非常に重要な役割を果たしている.
次回は主に数値計算論に関して説明する.
niltatsu
*1:Domingos, Pedro. "A unified bias-variance decomposition." Proceedings of 17th International Conference on Machine Learning. 2000.
機械学習概観 ~その① 学習フレームワーク論編~
今回は,機械学習という分野の概観,そしてそのフレームワークについて話していきたいと思う. なお,機械学習についての注意点・初心者が留意すべき点に関しては以下の記事を参考していただきたい.
さて,いざ機械学習の勉強を始めると,いきなり最尤推定とか最小二乗回帰など,「手法」の話が始まり,結局自分が今何をゴールにしており,何を勉強しているのか,そして最近よく聞く「ディープラーニンング」などの単語とどう関連するのか見えないことが多い. なので,自分なりの解釈になるかもしれないが,まず全体像から提示していきたいと思っている.
機械学習を構成する3要素
機械学習は,(あくまでも私見だが)大雑把に言うと以下の3つの方向性で研究されている.
- 学習フレームワーク論: 与えられた問題設定下で,どのような損失関数or報酬関数を設計し,それがどのような性質を持っているのかについての研究
- モデリング論: 予測などを行う際に,線形モデルやカーネルモデルなど,どのようなモデルやパラメータを選択すれば良いのか,もしくはそのモデルを使用した際の性質などを探求する研究
- 数値計算論: 1.の学習方法,2.のモデルの元で,より計算量の小さい(or計算時間の短い・メモリ使用量の少ない)最適化手法・数値計算法を探求する研究
この3つは不可分の関係にあり,個人的には機械学習という分野の「基底」を成しているように考えている. 以下では数回の記事に分けて,これら基底それぞれに対してもう少し詳細に見ていきたいと思う. 初回はまず学習フレームワーク論編.
学習フレームワーク論
学習フレームワークと一言で言っても,教師あり学習や分類・回帰など様々で,用語が乱立しているように思える. なので,以下ではそれらの用語についてまとめていく. まず学習法の大きな区分として
- 教師有り学習 (Supervised Learning)
- 半教師有り学習 (Semi-Supervised Learning)
- 教師無し学習 (Unsupervised Learning)
- 強化学習 (Reinforcement Learning)
がある(この区分に関しては個人的に若干疑問の部分もあるが...). これらの学習方法は,損失関数や報酬関数の設計が各々異なり,さらには定式化も全く異なる. なお今回の記事では,定式化などに関しては省略し,どのような問題設定があるのかについてのみ説明する.
教師有り学習 (Supervised Learning)
データ点$\bm{x}$(もしくは訓練入力と呼ぶ)と,それに対応する訓練出力$y$のペア$(\bm{x}, y)$が与えられたときに,$\bm{x}$から$y$の生成規則$f$を学習するフレームワークを教師有り学習と呼ぶ. つまり,$f(\bm{x}) \simeq y$であるような$f$を見つける,ということになる. この$\bm{x}$,$y$の与えられ方によって問題設定が異なってくるため,使用する損失関数・問題としての難易度が異なってくる. 教師あり学習の具体例を以下に示す.
二クラス分類 (Binary Classification)
二クラス分類とは,データ点$\bm{x}$が与えられた場合に,そのデータを$y = +1, y = -1$のいずれかに分類するタスクを指す.
この場合,訓練出力は「クラス」と呼ばれる.

多クラス分類 (Multi-class Classification)
多クラス分類とは,データ点$\bm{x}$が与えられた場合に,そのデータを$y = 1, 2, \ldots , K$のいずれか1つに分類するタスクを指す. 先ほどは2クラスだったのに対し,多クラスでは出力候補が$K>2$になっていると考えれば良い. わざわざ二クラス分類と多クラス分類を分けたのは,
- 難易度が全く違う (二クラスができれば多クラスも簡単に拡張できると思われがちだが,これは全く違う)
- 多ラベル分類と区別するため (後述)
多ラベル分類 (Multi-label Classification)
多クラス分類では,データ点$\bm{x}$を$y = 1, 2, \ldots , K$のうちいずれか1つのクラスに分類するが,多ラベル分類では,データ点を複数に分類することを許す. この場合,訓練出力は「ラベル」と呼ばれる. 「ラベル」という名称は,gmailのラベル機能のように,同じメールでも複数のラベルを許すことを考えればなんとなく意味は分かる. 「クラス」と「ラベル」は,出力が1つのみの場合は,同じ意味として考えることができる. ただあくまでも,
- 「クラス」は1つのみ属す
- 「ラベル」は複数を許容する
と考えればその差異について分かっていただけるだろう. 多ラベル分類で重要なのは,多くの場合で,ラベル同士にも相関関係などがあるという点(スノボが好きな人は,スキーが好きな可能性が高いなど). もちろんそれぞれのラベル1つずつに分割し,それぞれで二クラス分類を走らせることも可能だが,それはラベル同士の関係を無視しているので得策とは言えない. そこの関係性を利用するのが多ラベル分類ならではのポイントだろう. (ちなみにStructured Outputというのもあるが,今回は詳細は省く)
回帰 (Regression)
回帰とは,データ点$\bm{x}$が与えられた場合に,そのデータに関する何かしらの量$y$を推定するタスクを指す. 例えば,データ点として(経度,緯度,過去10日間の降水量,...)などの情報から明日の気温を当てるなどが回帰の例になる. 重要なのは,分類問題では属するクラスを推定するのに対し,回帰ではある特定の実数値を推定することがゴールになる.

上の図は回帰のイメージ図で,この図で分かって欲しいのは,回帰$\simeq$関数近似であること. つまり,赤色の曲線$f(x)$が学習したい真の曲線だとして,それを緑色の曲線$\hat{f}(x)$で近似することが回帰におけるゴールになる.
順序回帰 (Ordinal Regression)
順序回帰はアカデミアでは(分類や回帰などと比較して)少々マイナーな問題設定だが,実用上は非常に大切な問題設定である. 順序回帰とは,出力が順序尺度で,また出力候補が3つ以上のものを指す. 例として,アンケートを考えよう. アンケートで1から5を「大変不満」「不満」「どちらでもない」「満足」「大変満足」のような選択問題を見たことがあるだろう. これは,順序尺度(つまり1から5に優劣がある),かつ出力候補が3つ以上なので,新たなデータ点に対するアンケート結果を予測したい場合は,順序回帰を用いることになる. 普通の回帰と異なる点は,出力が実数値なのか,離散順序尺度なのか,だけである. また多クラス分類問題ではクラスは全て均質なのに対して,順序回帰で扱う出力は順序尺度なので優劣がある. これが多クラス分類と順序回帰の違う点である. そして最後に,出力候補が3つ以上であることを要請しているのは,出力候補が2つの場合は,出力が順序尺度であっても,二クラス分類として考えて解くことが可能になるからである.
ランキング (Ranking)
ランキング問題は上記の分類問題とは異なり,データ点ペア$(\bm{x}_1, \bm{x}_2)$が与えられ,訓練出力として${+1, 0, -1}$のいずれかが与えられる.ここで,
- 訓練出力が$+1$: $\bm{x}_1$は$\bm{x}_2$よりも好まれる
- 訓練出力が$-1$: $\bm{x}_2$は$\bm{x}_1$よりも好まれる
- 訓練出力が$0$: $\bm{x}_1$と$\bm{x}_2$は同様に好まれる
このように,「りんごよりももが好き」「ももよりバナナが好き」などの情報から,「梨とキウイのどっちが好きか」を推定する,という問題がランキング問題になる.
教師有り学習のまとめ
ここまでで,教師有り学習についての複数の問題設定について紹介した. 以下の表はそのまとめである.
| 問題設定 | 入力 | 出力候補 | 出力数 | 実例 |
|---|---|---|---|---|
| 二クラス分類 | $\bm{x}$ | ${+1, -1}$ | 1 | スパムフィルタなど |
| 多クラス分類 | $\bm{x}$ | ${1, 2, \ldots, K }$ | 1 | 手書き数字認識など |
| 多ラベル分類 | $\bm{x}$ | ${1, 2, \ldots, K }$ | 複数 | テキスト分析など |
| 回帰 | $\bm{x}$ | $\mathbb{R}$ | 1 | 株価予測 |
| 順序回帰 | $\bm{x}$ | 順序尺度 | 1 | アンケート結果予測 |
| ランキング | $(\bm{x}_1, \bm{x}_2)$ | ${ +1, 0, -1 }$ | 1 | ランキング予測 |
半教師有り学習 (Semi-Supervised Learning)
教師有り学習では,(データ点, 出力)の形の訓練データが与えられ,そこからデータ点と出力の関係を学習する. しかし現実問題として,全てのデータ点に対して出力(もしくはラベルなど)を付与すること(これをアノテーションと呼ぶ)は非常に大変である. そこで,少数の出力付きデータと(教師付きデータ)と,多数の出力無しデータ(教師無しデータ)だけから,データ点と出力の関係を学習するフレームワークを半教師有り学習と呼ぶ. 半教師有り学習は,教師有り学習と比較して,教師情報が不足しているので,一般的に学習の難易度は高くなる. また,今回は紹介しないが,半教師有り学習の亜種の弱教師有り学習と呼ばれる分野もあり(教師となる出力orラベルが,通常よりも少ない情報量をもっているような場合),こちらも近年注目を集めている.
教師無し学習 (Unsupervised Learning)
今までは,全て or 少数の(データ点, 出力)の形の訓練データが与えられることが前提であったが,究極の形として,訓練出力が全く与えられないような問題設定も考えられる. このフレームワークを教師無し学習と呼ぶ. この場合は,出力,すなわち教師に対応する情報がないので,性質が近いデータ点をいくつかのまとまり(これをクラスタと呼ぶ)にまとめることが学習に対応する. このようにクラスタにまとめるタスクをクラスタリングと呼ぶ. 教師無し学習というと,ほぼほぼクラスタリングを指すので,教師無し学習$\simeq$クラスタリングと考えて良い.
強化学習 (Reinforcement Learning)
強化学習は今までの学習法とは一味違うフレームワークとなっている. 強化学習では,以下の用語が使用される(循環定義になってるし,厳密な定義になっていないが,そこはなんとなくで良いので察して...w).
- エージェント: 行動主体のこと
- 環境: エージェントを取り巻く周囲の状態などを指す
- 状態: 今現在の環境がどのようになっているのかを指す
- 行動: エージェントが現在の状態・環境に対して起こす行動を指す
- 報酬: エージェントが現在の状態・環境に対して,特定の行動を起こした場合に受け取る利益を指す
上の用語を用いると,強化学習とは,「ある環境内におけるエージェントが,現在の状態を観測し,将来の期待報酬を最大化するような行動を学習する」フレームワークだと言える. 強化学習は人間の成長過程と非常に似ている. もちろん学校に入ってしまえばそこには教師がいるので,そこでは教師有り学習が行われている,と考えることができる. しかし,より幼い子供は,そもそも何をするのが正しいのか知らないので,とりあえず行動を起こす. そしてお母さんに褒められたり,叱られたり(報酬)することで,すべき行動すべきでない行動を学んでいく. これはまさしく強化学習であると言える.
また強化学習の一種として,バンディットと呼ばれる問題設定もあるので,気になる方は調べると良い.
まとめ
今回は機械学習の3要素の内,主に学習フレームワーク論についての概要を与えた. 学習に関する異なる問題設定は,異なる定式化を与え,その研究は非常に盛んに行われている. NIPSやICMLなどのトップ会議には,今でも新たな問題設定・新たな学習フレームワークに関する論文が提出されており,非常に大切な分野であることが伺える.
次回は主にモデリング論に関して説明する.
niltatsu