これなら分かるEMアルゴリズム①

今回は主にEMアルゴリズムについて． 筆者が初めてEMアルゴリズムを見たのは学部3年の機械学習の授業の頃． そのときは教師無し学習の話からスタートし，まずは$k$-meansアルゴリズム． 「ふむふむ，クラスタ数を事前に決めといて，平均を近くのデータ点を使ってどんどん更新するのね，分かりやすい．」

そのままの流れでEMアルゴリズムへ． そこで難易度が急激アップ． 「潜在変数」「$Q$関数」「寄与率」などの単語が急にたくさん出てきて大混乱． しかも途中の計算が慣れないとそこそこ大変なので，結局何をやっているのかさっぱり．

しばらく経って，様々な場面でEMアルゴリズムを拝見し，自分なりに納得のいく説明の仕方ができたので，ここで書こうと思う． 個人的には，初心者にいきなり「潜在変数」や「$Q$関数」などの概念を出しても全く分からない原因になるだけだと思っている． これらの用語を使わなくても，EMアルゴリズムは説明可能である． なので，以下ではまずこれらの用語を用いない導出を行う(そのため，他の記事や本などと比較して，少々異なる理論構成になっているかも)． ただし，いざ書いてみるとかなりの長さになるので，複数回に分けて紹介しようと思う． 今回は混合正規分布の最尤推定によるクラスタリング手法から．

問題設定

データ$\mathcal{D} = \{ \bm{x}_i \}_{i=1}^n \subset \mathbb{R}^d$が与えられたとして，これらを$K$個のまとまり(クラスタ)にクラスタリングすることを考える． 混合分布モデルでは，データの分布$p(\bm{x} | \Theta)$を以下のような形でモデリングする: $$ p(\bm{x} | \Theta) = \sum_{k=1} ^K \pi_k p(\bm{x} | \bm{\theta}_k). $$ ここで，$\pi_k$は$\sum_{k=1} ^K \pi_k = 1$を満たし，$\Theta = \{ \pi_1, \ldots, \pi_K, \bm{\theta}_1, \ldots, \bm{\theta}_K \}$とする． 特に，$p(\bm{x} | \bm{\theta}_k)$が正規分布，すなわち$p(\bm{x} | \bm{\theta}_k) = \mathcal{N} (\bm{x} | \bm{\mu}_k, \varSigma_k)$の場合，混合正規分布モデルと呼ばれる． 当たり前だが，この場合$\bm{\theta}_k = \{ \bm{\mu}_k, \varSigma_k \}$となる． 混合分布モデルの気持ちとしては...

• データの分布は$K$個のクラスタによって生成されており，$k$番目のクラスタの分布は$p(\bm{x} | \bm{\theta}_k)$．各クラスタがクラスに対応する多クラス分類問題で例えるなら，$p(\bm{x}|y=k)$に相当．
• $\pi_k$は混合係数と呼ばれ，各クラスタの「重み」のようなもの．各クラスタがクラスに対応する多クラス分類問題で例えるなら，$p(y=k)$に相当．

最終的なゴールとしては，$\Theta$の各パラメータを求まれば良い，ということになる． これを実行するためには最尤推定，すなわち，以下の最適化問題を$\Theta$について解けば良いということになる: $$ \max_{ \bf{1}^\top \bm{\pi} = 1} \sum_{i = 1}^n \log p(\bm{x}_i | \Theta) = \max_{ \bf{1}^\top \bm{\pi} = 1} \sum_{i = 1}^n \log \left( \sum_{k=1} ^K \pi_k p(\bm{x}_i | \bm{\theta}_k) \right). \tag{1} $$

ぶっちゃけ問題設定としてはこれ以上もこれ以下でもない． 何かしらの手段を用いて最適化問題(1)が解ければクラスタリング大成功である． しかし，世の中そんな甘くはない... 右辺を見て欲しい． $\log$関数の中に和が入っている． 「これが何だよ」というわけだが，想像してほしい． この最適化問題を解くためには，ラグランジュ乗数を導入し，ラグランジュ関数を微分して$0$を解けば良いわけだ． しかし$\log$関数の中に和があると，微分して得られる関数は分数関数で，分母に和が残る形になる． 更に言えば，$\pi_k$もしくは$\bm{\theta}_k$について微分したのにも関わらず，微分して得られる関数は$\pi_1, \ldots, \pi_K, \bm{\theta}_1, \ldots, \bm{\theta}_K$全部が絡み合った分数連立方程式になっているわけだ． こんなの解けっこない． つまり，この最適化問題を直接解くのを諦める他ない．

そこで考案されたのがEMアルゴリズムだ．

Jensenの不等式を用いた下界の導出

さて，最適化問題(1)を解きたいけど解けない． このような場合，良く用いられるのが「別の解きやすい関数を考え，それを解くことで間接的に元の問題を解く」という方法である． 今回の場合，$\log$関数の中に和があるのが難しさの元凶なので，これを崩せさえすれば良い． 「$\log$関数の中に和」の形に出くわしたときに役に立つのがJensenの不等式である．

Jensenの不等式

定理: (Jensenの不等式) $c_k$を$c_k \geq 0, \sum_{k=1}^K c_k = 1$を満たす実数とし，$x_k\ (k=1, \ldots, K)$を任意の実数とする．このとき，上に凸な関数$f$に対して，以下の不等式が成立する: $$ f \left( \sum_{k=1}^K c_k x_k \right) \geq \sum_{k=1}^K c_k f ( x_k ). \tag{2} $$ 等号成立条件は$x_1 = \cdots = x_K$である．

証明に関しては以下の図を見れば明らかであろう．

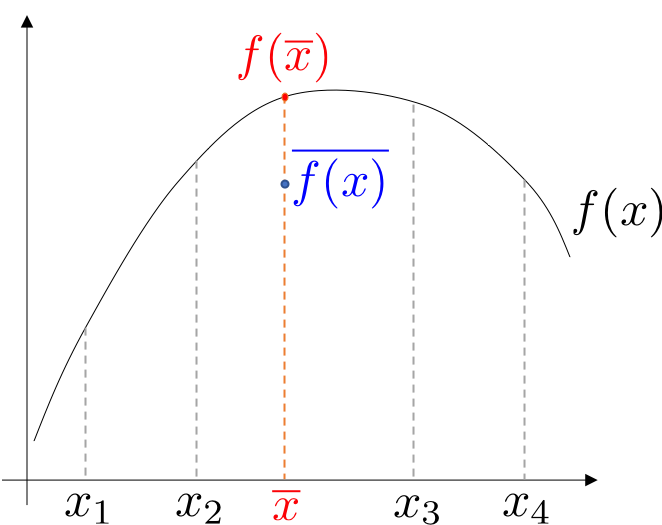
さて，このJensenの不等式を使うと何が良いのか． 不等式(2)における$f$を$\log$関数として考えると，左辺はまさしく最尤推定の最適化問題で現れる$\log$関数の中に和がある形になることが分かるだろう． つまり，「和の$\log$ $\geq$ $\log$の和」なので，「$\log$の和」が「和の$\log$」の下界を与える． 最適化問題(1)の下界を最大化することで，最適化問題(1)そのものも大きくしていこう，というのがEMアルゴリズムのアイデアである． さて以下では，対数尤度の式に対していかにしてJensenの不等式を適用していくのか見ていこう．

作戦1: $\pi_k$を$c_k$とみなす

まず容易に思いつくのが「$\pi_k$を$c_k$とみなす」という作戦である． これを実際にやってみると， $$ \sum_{i = 1}^n \log \left( \sum_{k=1} ^K \pi_k p(\bm{x}_i | \bm{\theta}_k) \right) \geq \sum_{i = 1}^n \sum_{k=1} ^K \pi_k \log p(\bm{x}_i | \bm{\theta}_k) $$ となる． いまやりたいことは対数尤度の下界の最大化なので，以下の最適化問題を解けば良いことになる: $$ \max_{\bf{1}^\top \bm{\pi} = 1} \sum_{i = 1}^n \sum_{k=1} ^K \pi_k \log p(\bm{x}_i | \bm{\theta}_k). $$ さて，これを実際に解いていこう． いまラグランジュ乗数$\alpha$を導入すると，ラグランジュ関数は以下のように書ける: $$ L(\Theta, \alpha, \mathcal{D}) = \sum_{i = 1}^n \sum_{k=1} ^K \pi_k \log p(\bm{x}_i | \bm{\theta}_k) + \alpha \left( \sum_{k=1}^K \pi_k - 1 \right). $$ 最適性条件から，$\bm{\theta}_k, \pi_k, \alpha$について微分すると，以下のようになる． $$ \begin{aligned}\tag{3} \dfrac{\partial}{\partial \bm{\theta}_k} L(\Theta, \alpha, \mathcal{D}) &= \sum_{i = 1}^n \pi_k \dfrac{\partial}{\partial \bm{\theta}_k} \log p(\bm{x}_i | \bm{\theta}_k) = 0, \\ \dfrac{\partial}{\partial \pi_k} L(\Theta, \alpha, \mathcal{D}) &= \sum_{i = 1}^n \log p(\bm{x}_i | \bm{\theta}_k) + \alpha = 0, \\ \dfrac{\partial}{\partial \alpha} L(\Theta, \alpha, \mathcal{D}) &= \sum_{k=1}^K \pi_k -1 = 0. \end{aligned} $$ さて，混合正規分布の場合，$p(\bm{x} | \bm{\theta}_k) = \mathcal{N} (\bm{x} | \bm{\mu}_k, \varSigma_k)$であるので，これを実際に代入すると， $$ \begin{aligned} \hat{\bm{\mu}}_k &= \dfrac{1}{n} \sum_{i=1}^n \bm{x}_i, \\ \hat{\varSigma}_k &= \dfrac{1}{n} \sum_{i=1}^n (\bm{x}_i - \hat{\bm{\mu}}_k) (\bm{x}_i - \hat{\bm{\mu}}_k)^\top, \\ \hat{\pi}_k &= \dfrac{1}{K}. \end{aligned} $$ あれれ〜？おかしいな... これって結局全部のクラスタで同じパラメータを共有しているから，「混合」正規分布になってなくない？ てかただの1つの正規分布の最尤推定やん... ということでこの作戦は失敗...

作戦2: 新たな$q_k^{(i)}$を作り出す

さて，作戦1は失敗に終わった． 一回ここでその原因について反省してみよう． 方程式(3)を見ると，最適解が$k$に依存しないような形になってしまっている． $k$によらないということは，変な話，各クラスタに「個性」がないのである． ゆえに最適解が$k$に依存する形，つまり各々の最適解に「個性」を持たせれば良い． そこで新たな変数として，$q_k^{(i)}$を考え，以下のように「1をかける」: $$ \sum_{i = 1}^n \log \left( \sum_{k=1} ^K \pi_k p(\bm{x}_i | \bm{\theta}_k) \right) = \sum_{i = 1}^n \log \left( \sum_{k=1} ^K q_k^{(i)} \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right). $$ ただし「諸事情により」，$\sum_{k=1}^K q_k^{(i)} = 1$なる制約を設ける． 直感的にはこの制約がないと，$q_k^{(i)}$をそれぞれ無限大に大きくすればいくらでも目的関数が大きくなるので，最適化問題としての意味がなくなってしまう． さて，この右辺に対してJensenの不等式を適用すると， $$ \sum_{i = 1}^n \log \left( \sum_{k=1} ^K q_k^{(i)} \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right) \geq \sum_{i = 1}^n \sum_{k=1} ^K q_k^{(i)} \log \left( \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right) $$ という下界が得られる． よって最終的に私たちが解きたい最適化問題は以下のようになる: $$ \max_{\bf{1}^\top \bm{\pi}=1, \bf{1}^\top \bm{q}^{(i)} = 1} \sum_{i = 1}^n \sum_{k=1} ^K q_k^{(i)} \log \left( \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right). \tag{4} $$ 「この$q_k^{(i)}$を導入すると本当に$k$に依存する最適解が得られるの？」 この疑問については以下で解消しよう．

下界の最適化

ここからは最適化問題(4)を解いていく． この手の最適化問題は上の(3)式でやったように，ラグランジュ乗数を導入してラグランジュ関数の最適化に持ち込むのが定石である． ラグランジュ乗数$\alpha, \bm{\beta}$を導入すると， $$ \begin{aligned} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) = &\sum_{i=1}^n \sum_{k=1}^K q_k^{(i)} \log \left( \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right)\\ &+ \alpha \left( \sum_{k=1}^K \pi_k -1 \right) + \sum_{i=1}^n \beta_i \left( \sum_{k=1}^K q_k^{(i)} -1 \right) \end{aligned} $$ うーん，長い式になってしまった...が仕方がない． さて，ここからは少々大変な作業になるが，実際に$\bm{\theta}_k, \pi_k, \alpha, \beta_i, q_k^{(i)}$で微分していくと: $$ \begin{aligned} \tag{5} \dfrac{\partial}{\partial \bm{\theta}_k} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) &= \sum_{i=1}^n q_k^{(i)} \dfrac{\partial}{\partial \bm{\theta}_k} \log p(\bm{x}_i | \bm{\theta}_k) = 0, \\ \dfrac{\partial}{\partial \pi_k} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) &= \sum_{i=1}^n \dfrac{q_k^{(i)}}{\pi_k} + \alpha = 0, \\ \dfrac{\partial}{\partial \alpha} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) &= \sum_{k=1}^K \pi_k -1 = 0, \\ \dfrac{\partial}{\partial \beta_i} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) &= \sum_{k=1}^K q_k^{(i)} - 1 = 0, \\ \dfrac{\partial}{\partial q_k^{(i)}} L(\Theta, \alpha , \bm{\beta}, \bm{q}, \mathcal{D}) &= \log \left( \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{q_k^{(i)}} \right) - 1 + \beta_i = 0, \end{aligned} $$ となる． さて，方程式(5)を眺めてみよう． うーん...どこから解き始めれば良いことか... まず結論から言おう． これはこのままでは解析的には解けない． 厄介な理由は$q_k^{(i)}$が5本の式中4本に現れていて，非常に複雑に絡み合っている点にある．

元々は最適化問題(1)が解きにくいからJensenの不等式とか使って苦労して別の最適化問題(4)を作ったのに，それがまた解けないとは何事じゃ！？w これはごもっともな意見だし，筆者もこれに悩まされた． ただ実は，元の最適化問題(1)は「ほぼ解けない」のだが，最適化問題(4)(つまり方程式(5))を解く手段はまだ残されている．

最適化の作戦

では方程式(5)をどのように解けば良いのか． もう一度言うが，方程式(5)が厄介なのは$q_k^{(i)}$がいたるところに現れているのが問題なのである． じゃあ，$q_k^{(i)}$を固定してしまえば良い． もう少し正確に言えば，

• $q_k^{(i)}$を既知にして$\Theta$について方程式(5)を解く
• $\Theta$を既知にして$q_k^{(i)}$について方程式(5)を解く

ようにする． $\Theta$と$q_k^{(i)}$のいずれか片方を固定してもう片方を解くことで，どんどん方程式の解に近づけようという作戦である． このように，片方の変数を固定してもう片方の変数について最適化するようなアルゴリズムを交互最適化アルゴリズムと呼ぶ． これは片方の変数orパラメータがもう片方の変数orパラメータに複雑に絡み合っている場合に有効な手法だ． では以下でそのこの交互最適化を実行していく．

$q_k^{(i)}$の最適化

まずは$\Theta$を固定して$q_k^{(i)}$について解く． これを実行するには方程式(5)の5本目の式に着目する(他の式は$q_k^{(i)}$についての和分になっているので解けない...)． これを$q_k^{(i)}$について解くと， $$ \begin{aligned} \hat{q}_k^{(i)} = \exp(1-\beta_i) \pi_k p(\bm{x}_i | \bm{\theta}_k) \end{aligned} $$ が得られる． ここで方程式(5)の4本目の式を利用すれば， $$ \begin{aligned} \hat{q}_k^{(i)} = \dfrac{\pi_k p(\bm{x}_i | \bm{\theta}_k)}{\sum_{k'=1}^K \pi_{k'} p(\bm{x}_i | \bm{\theta}_{k'})} \end{aligned} $$ と求めることができる． さて，ここでこの式の意味について考えてみる． $K$クラスの多クラス分類問題の場合と照らし合わせると，$\pi_k = p(y=k)$，$p(\bm{x} | \bm{\theta}_k) = p(\bm{x}|y=k)$などと対応づけが可能である． ゆえにベイズの定理から， $$ \begin{aligned} \hat{q}_k^{(i)} = \dfrac{p(y=k) p(\bm{x}_i | y=k)}{\sum_{k'=1}^K p(y=k) p(\bm{x}_i | y=k')} = p(y=k|\bm{x}_i) \end{aligned} $$ が成立する． $q_k^{(i)}$は「$i$番目のデータが$k$番目のクラスタどのくらい寄与しているのか」を表しているので，寄与率と呼ばれる．

$\Theta$の最適化

さて，以上で得られた$q_k^{(i)}$を固定して次に$\Theta$について解く．

$\pi_k$の最適化

これは方程式(5)の2本目の式に着目する． これを$\pi_k$について解くと， $$ \begin{aligned} \hat{\pi}_k = - \dfrac{1}{\alpha} \sum_{i=1}^n q_k^{(i)} \end{aligned} $$ が得られる． ここで方程式(5)の3本目の式を利用すれば， $$ \begin{aligned} \hat{\pi}_k = \dfrac{1}{n} \sum_{i=1}^n q_k^{(i)} \end{aligned} $$ と求めることができる． さて，ここでこの式の意味について考えてみる． $K$クラスの多クラス分類問題の場合と照らし合わせると， $$ \begin{aligned} \hat{\pi}_k = \dfrac{1}{n} \sum_{i=1}^n q_k^{(i)} = \dfrac{1}{n} \sum_{i=1}^n p(y=k|\bm{x}_i) \simeq \int p(y=k|\bm{x}) p(\bm{x}) \mathrm{d} \bm{x} = p(y=k) \end{aligned} $$ となり，$\pi_k = p(y=k)$の直感とも合致する．

$\theta_k$の最適化

これは方程式(5)の1本目の式に着目する． 一般形の形だとここまでしか解けない． ただし，混合正規分布モデルの場合，$\mu_k$について解くと， $$ \begin{aligned} \hat{\bm{\mu}}_k = \dfrac{\sum_{i=1}^n q_k^{(i)} \bm{x}_i}{\sum_{i=1}^n q_k^{(i)}} \end{aligned} $$ と求めることができる． また，$\varSigma_k$について解くと， $$ \begin{aligned} \hat{\varSigma}_k = \dfrac{\sum_{i=1}^n q_k^{(i)} (\bm{x}_i - \hat{\bm{\mu}_k}) (\bm{x}_i - \hat{\bm{\mu}_k})^\top}{\sum_{i=1}^n q_k^{(i)}} \end{aligned} $$ が得られる． さて，ここでこれらの式の意味について考えてみる． $K$クラスの多クラス分類問題の場合と照らし合わせると， $$ \begin{aligned} \hat{\bm{\mu}}_k &= \dfrac{\sum_{i=1}^n q_k^{(i)} \bm{x}_i}{\sum_{i=1}^n q_k^{(i)}} = \dfrac{\dfrac{1}{n} \sum_{i=1}^n q_k^{(i)} \bm{x}_i}{\dfrac{1}{n} \sum_{i=1}^n q_k^{(i)}} \\ &\simeq \dfrac{\int \bm{x} p(y=k|\bm{x}) p(\bm{x}) \mathrm{d} \bm{x}}{p(y=k)} = \int \bm{x} p(\bm{x}|y=k) \mathrm{d} \bm{x} = \mathbb{E}_{p(\bm{X}|Y=k)} \left[ \bm{X} \right] \end{aligned} $$ となり，$\bm{\mu}_k = \mathbb{E}_{p(\bm{X}|Y=k)} \left[ \bm{X} \right]$の直感とも合致する． また$\varSigma_k$についても同様に計算すれば$\mathbb{E}_{p(\bm{X}|Y=k)} \left[ (\bm{X}-\bm{\mu}_k) (\bm{X}-\bm{\mu}_k)^\top \right]$のようになる．

$q_k^{(i)}$を導入すると本当に$k$に依存する最適解が得られるの？

さてここで$q_k^{(i)}$を導入した際に生じた上記の疑問について答えよう． ずばり，答えはyesである． 実際に上の$\bm{\mu}_k, \varSigma_k, \pi_k$の結果を見て欲しい． $q_k^{(i)}$がはさまってことによって，($\bm{q}_k$が互いに異なれば)当然ながら$\bm{\mu}_k, \varSigma_k, \pi_k$の推定値も異なるのである． つまり，この$q_k^{(i)}$はいわば「個性」をもたらす役割を果たしているのである．

アルゴリズムのまとめ

最後に一回このアルゴリズムについてまとめていこう． 思考の流れとしては以下のようになる:

1. 混合分布モデルの最尤推定 = 最適化問題(1)を解きたい $\Rightarrow$ でも解けない
2. Jensenの不等式を用いて下界を求め解きやすい形に $\Rightarrow$ 最適化問題(4)を解けば良い
3. 最適化問題(4)を解く = 方程式(5)を解く $\Rightarrow$ このままでは解けない
4. $\Theta$と$q_k^{(i)}$の交互最適化に持ち込む

こう考えるとアルゴリズムの導出の思考過程も非常に分かりやすいのではないのでしょうか．

さて，最後に以下に混合分布モデルのアルゴリズムについてまとめる．

EMアルゴリズム(混合分布モデル)

1. 初期化: $\Theta, \bm{q}$を適当に初期化
2. While 収束していない do:
   1. 現在の$\Theta$を用いて$\bm{q}$を計算
   2. 現在の$\bm{q}$を用いて$\Theta$を計算

次回予告

さて，今回は主にEMアルゴリズムの最も基本的な部分について解説した． お分かりいただけただろうか... ただ今回お見せしたのは，EMアルゴリズムのほんの氷山の一角である． 次回はEMアルゴリズムのより詳細な一般論について述べる．

niltatsu